Question
Question: A wire carrying current \( I \) has the shape as shown in the adjoining figure. Linear parts of the ...
A wire carrying current I has the shape as shown in the adjoining figure. Linear parts of the wire are very long and parallel to the x - axis while the semicircular portion of the radius R is lying in Y – Z plane. The magnetic field at a point O is
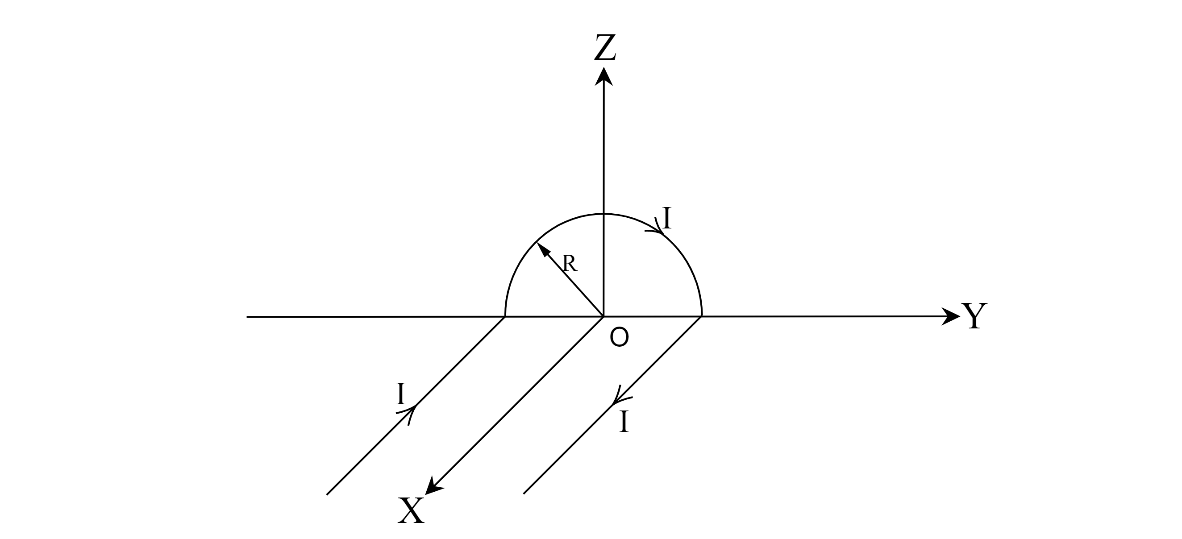
Solution
Hint : As the magnetic field is a vector quantity, we need to consider both – magnitude as well as the direction of the magnetic field. To find the magnitude of the magnetic field, the formulas for infinitely long straight wire and circular ring can be used. The direction of the magnetic field can be found by the Right-Hand Thumb rule.
Complete Step By Step Answer:
Let us divide the given arrangement so that it is easier to find the magnitude and direction of the magnetic field.
Let the long wire carrying the current I towards the semi-circular loop be a component 1 .
Let the semi-circular loop be a component 2 .
Let the long wire carrying the current I away from the semi-circular loop be a component 3 .
Now, consider the component 1 ,
We know that the magnitude of the magnetic field of an infinitely long wire can be calculated as,
B=2πaμ0I , where a is the perpendicular distance of the point (which lies outside the wire) at which the magnetic field is to be found.
Now, the wire is very long, hence its one end is considered infinite. But its other end intersects with the loop, which makes the end finite.
Hence, as the wire is infinitely long in only one direction, it can be considered as a semi-infinitely long wire.
If the wire was infinite, it would move in both directions starting at some origin point. But here, the wire is only moving in one direction, hence the semi-infinite wire is considered as half of the infinite wire.
Hence, the magnitude of the magnetic field for the semi-infinite wire can be considered as half of the magnitude for an infinitely long wire.
∴B1=4πaμ0I
The distance of the point O from the wire is equal to the radius of the semi-circular loop.
∴B1=4πRμ0I
Now, by Right Hand Rule, we point the thumb in the direction of current, and the direction in which the wrapped fingers point gives the direction of the magnetic field.
Here, the wrapped fingers point in a downward direction when they come to the point O
Hence, the downward direction is the negative Z - direction.
∴B1=4πRμ0I(−k^)
Similarly, consider the component 3 which is also infinite in one direction i.e. semi-infinite.
Hence, the magnitude is the same as the component 1
∴B3=4πRμ0I
For the direction of the magnetic field, when we point the thumb in direction of the current, the wrapped fingers point in a negative Z direction at the point O
∴B3=4πRμ0I(−k^)
Now, for the component 2 ,
We know that the magnetic field of a circular ring with n turns at the center is given as,
B=2Rμ0nI
Here, we have a semi-circular ring with one turn, hence the magnetic field is half of the field for the circular ring.
∴B2=4Rμ0I
For the direction of the magnetic field, when we point the thumb in the direction of the current, the wrapped fingers point inside the paper at the point O which is the negative X - direction.
∴B2=4Rμ0I(−i^)
Now, taking the sum of fields of all the components.
∴B=B1+B2+B3
Substituting the derived values,
∴B=4πRμ0I(−k^)+4Rμ0I(−i^)+4πRμ0I(−k^)
∴B=4πR2μ0I(−k^)+4Rμ0I(−i^)
Taking L.C.M.,
∴B=4πR2μ0I(−k^)+μ0πI(−i^)
∴B=−4πRμ0I(2k^+πi^)
This is the resultant magnetic field at the point O .
Note :
The magnetic field of the semi-infinite wire can also be found from the formula for the finite wire. The angle made by the perpendicular line and line joining the origin of wire and the point is 0∘ . And the angle made by the perpendicular line and the line joining the infinite end with the point can be considered as 90∘
∴B=4πRμ0I[sin90∘+sin0∘]
