Question

A window of a house is h meter above the ground. From the widow, the angles of elevation and depression of the top and bottom of another house situated on the opposite side of the lane are found to be $\alpha$ and $\beta$ respectively. Prove that the height of the house is $h\left( 1+\tan \left( \alpha \right)\cot \left( \beta \right) \right)$ meters.

Answer 1

Hint:We will use the concept of elevation and depression to draw the diagram. The elevation means watching any object above the height of horizontal vision whereas depression is to see below the height of horizontal vision. Here, horizontal vision means when we see exactly straight in the front. Also, we will use the trigonometric formula $\tan \left( \theta \right)=\dfrac{\text{Perpendicular}}{\text{Base}}$.

Complete step-by-step answer:
The diagram for the question is given below.

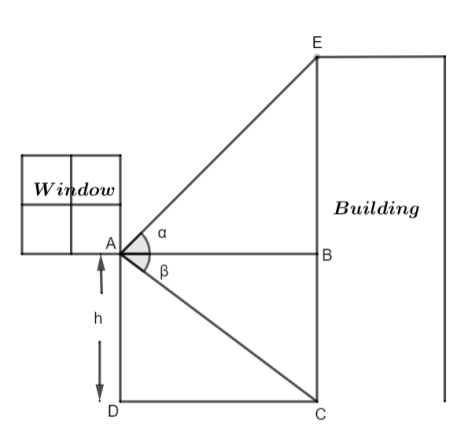
In the diagram we can clearly see that the window is at the point A and the height of AD is h meters. We consider the horizontal vision as the line AB. Therefore, the angle of elevation of the top of the building which is in front of the window at point E is given by $\angle EAB$ = $\alpha$. Moreover, the angle of depression to the bottom of the front building at point C is $\angle BAC$ = $\beta$.
Since, BC is parallel and opposite AD. Therefore, AD = BC = h meters. Now, we will apply trigonometric formula on $\angle EAB$ = $\alpha$ which is given by $\tan \left( \theta \right)=\dfrac{\text{Perpendicular}}{\text{Base}}$. Thus, we have $\begin{aligned} & \tan \left( \alpha \right)=\dfrac{EB}{AB} \\\ & \Rightarrow AB=\dfrac{EB}{\tan \left( \alpha \right)}...(i) \\\ \end{aligned}$
Also by applying the same trigonometric formula on $\angle BAC$ = $\beta$ we get $\tan \left( \beta \right)=\dfrac{BC}{AB}$. Since, BC = h meters therefore,
$\begin{aligned} & \tan \left( \beta \right)=\dfrac{h}{AB} \\\ & \Rightarrow AB=\dfrac{h}{\tan \left( \beta \right)}...(ii) \\\ \end{aligned}$
Now equating equation (i) and (ii) we get,
$\begin{aligned} & \dfrac{EB}{\tan \left( \alpha \right)}=\dfrac{h}{\tan \left( \beta \right)} \\\ & \Rightarrow EB=\dfrac{h\tan \left( \alpha \right)}{\tan \left( \beta \right)} \\\ \end{aligned}$
Now we can know that the height of the building which is in front of the window is EC = EB + BC, where BC = h meters. Therefore, we have
$\begin{aligned} & EC=EB+BC \\\ & \Rightarrow EC=\dfrac{h\tan \left( \alpha \right)}{\tan \left( \beta \right)}+h \\\ & \Rightarrow EC=h\left( \dfrac{\tan \left( \alpha \right)}{\tan \left( \beta \right)}+1 \right) \\\ \end{aligned}$
Now we use the formula $\tan \left( \beta \right)=\dfrac{1}{\cot \left( \beta \right)}$ results into,
$\begin{aligned} & EC=h\left( \dfrac{\tan \left( \alpha \right)}{\tan \left( \beta \right)}+1 \right) \\\ & \Rightarrow EC=h\left( \tan \left( \alpha \right)\cot \left( \beta \right)+1 \right) \\\ \end{aligned}$
Hence, the height of the building $EC=h\left( \tan \left( \alpha \right)\cot \left( \beta \right)+1 \right)$ is proved.

Note: Alternatively we could have used the trigonometric formula $\cot \left( \theta \right)=\dfrac{\text{base}}{\text{perpendicular}}$ to the angle of elevation which is $\angle EAB$ = $\alpha$. Therefore, we could have got $\cot \left( \alpha \right)=\dfrac{AB}{EB}$ and solved as usual. Similarly, the angle of deviation is solved. But the last result should be changed as $\cot \left( \alpha \right)=\dfrac{1}{\tan \left( \alpha \right)}$.