Question

A window is in the shape of a rectangle surmounted by a semicircle opening. The total perimeter of the window is $10m$ . Find the dimension of the window to admit maximum through the whole opening.

Answer 1

The word surmounted means it is on top of a rectangular window that has a semi-circle top. If a function is double differentiated then it can give you a maximum or minimum point and the perimeter of the circle is $(\pi r)$ , whereas that of the rectangle is $(length + base)$ .

Complete step-by-step solution:
Given: Perimeter of the window is $10m$ .

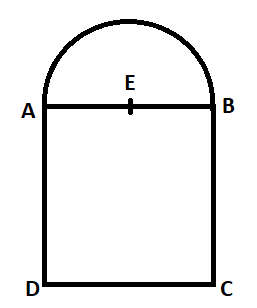
Let the radius of the semi-circle, length and breadth of the rectangle be $r,x$ and $y$ respectively.
Therefore, from the figure we can determine that
$AE = r$
$AB = x = 2r$ , since the semi-circle is mounted over the rectangle ---- (1)
$AD = y$
Now, according to the question,
Perimeter of the window is $10m$.
$\Rightarrow x + 2y + \pi r = 10 \\\ \Rightarrow (2r + \pi r) - 10 = - 2y \\\ \Rightarrow 2y = 10 - (\pi + 2)r \\\$
$y = \dfrac{{\left( {10 - (\pi + 2)r} \right)}}{2}$ -------- (2)
To admit the maximum amount of light, the area of the window should be maximum. Assuming the area of the window as, area of the rectangle $+$ area of the semicircle.
$A = xy + \dfrac{{\pi {r^2}}}{2} \\\ \Rightarrow A = (2r)\left( {\dfrac{{10 - (\pi + 2)r}}{2}} \right) + \dfrac{{\pi {r^2}}}{2} \\\ \Rightarrow A = 10r - \pi {r^2} - 2{r^2} + \dfrac{{\pi {r^2}}}{2} \\\ \Rightarrow A = 10r - 2{r^2} - \dfrac{{\pi {r^2}}}{2} \\\$
Condition for maxima and minima is to differentiate the area,
$\dfrac{{dA}}{{dr}} = 0 \\\ \Rightarrow 10 - 4r - \pi r = 0 \\\ \Rightarrow r = \dfrac{{10}}{{4 + \pi }} \\\$
Now, double differentiating the area, we have
$\dfrac{{{d^2}A}}{{d{r^2}}} = - 4 - \pi < 0$
For the $r = \dfrac{{10}}{{(4 + \pi )}}$ , $A$ will be maximum here $A$ stands for area.
Length of the rectangular part $= \dfrac{{20}}{{(4 + \pi )}}m$ [from equation (1)]
Breadth of the rectangular part $= \dfrac{{10 - (\pi + 2)r}}{2}m$ [from equation (2)]
$\Rightarrow y = \dfrac{{10 - \dfrac{{(\pi + 2)10}}{{4 + \pi }}}}{2} \\\ \Rightarrow y = \dfrac{{10}}{{4 + \pi }} \\\$
Thus, the dimension of the window which will admit the maximum amount of light is
$x = \dfrac{{20}}{{4 + \pi }}m$ and $y = \dfrac{{10}}{{4 + \pi }}m$

Note: In this type of questions students often make the mistake that they do not double differentiate and take the area of the rectangle part as $2(x + y)$ which is incorrect. Do not make this mistake.