Solveeit Logo
Login

Question

Question: A window is in the form of a rectangle above which there is a semicircle. If the perimeter of the wi...

A window is in the form of a rectangle above which there is a semicircle. If the perimeter of the window is p meter, show that the window will receive maximum possible light only when the radius of semicircles is pπ+4\dfrac{p}{{\pi + 4}}.

Explanation

Solution

This question is solved with the help of the property of the circle and rectangle.Since there are both the figures involved in the question,we will make use of this property and solve this question.

Complete step by step solution:
A circle is a locus of points equidistant from a given point which is the centre of the circle. The common distance from the Centre of a circle to its point is called a radius.

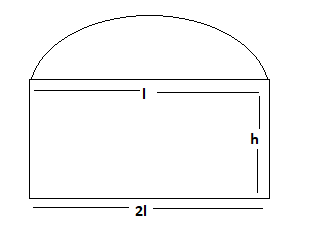
The perimeter of a semicircle is half of the circle. As the perimeter of a circle is 2πr or πd. So, the perimeter of a semicircle is 1/2 (πd) or πr, where r is the radius.
P is the perimeter of the windows.
l→l \to length of the window
h→h \to height of the windows
Use the formula of perimeter
2l+2h+λl=p2l + 2h + \lambda l = p
⇒(2+π)l+2h=p\Rightarrow \left( {2 + \pi } \right)l + 2h = p
⇒2h=p−(2+π)l\Rightarrow 2h = p - \left( {2 + \pi } \right)l
⇒h=p−(2+π)l\Rightarrow h = p - \left( {2 + \pi } \right)l
⇒h=p−(2+θ)l2\Rightarrow h = \dfrac{{p - \left( {2 + \theta } \right)l}}{2}
Use the area formula: (1)
Area = 2hl+πl222hl + \dfrac{{\pi {l^2}}}{2} (2)
Substitute the value of h in the eq.
Area = 2l\left\\{ {\dfrac{{p - \left( {2 + \theta } \right)l}}{\pi }} \right\\} + \dfrac{{\pi {l^2}}}{2}
Area = l[P−(2+π)l]+πl22l\left[ {P - \left( {2 + \pi } \right)l} \right] + \dfrac{{\pi {l^2}}}{2}
⇒p−2(2+π)l+πl\Rightarrow p - 2\left( {2 + \pi } \right)l + \pi l
⇒pl(π−4−2π)\Rightarrow pl\left( {\pi - 4 - 2\pi } \right)
⇒l(π−4−2π)=−p\Rightarrow l\left( {\pi - 4 - 2\pi } \right) = - p
⇒l(π−4−2π)=−p\Rightarrow l\left( {\pi - 4 - 2\pi } \right) = - p
⇒l(−π−4)=−p\Rightarrow l\left( { - \pi - 4} \right) = - p
⇒l=+p+(π+4)\Rightarrow l = \dfrac{{ + p}}{{ + \left( {\pi + 4} \right)}}
l=pπ+4l = \dfrac{p}{{\pi + 4}}

Note: When a circle is cut into two halves or when the circumference of a circle is divided by 2, we get Semi-circular shape.
Since a semicircle is half that of a circle, hence the area will be half that of a circle.
The area of a circle is the number of square units inside that circle.