Question

A wheel with radius $45\,{\text{cm}}$ rolls without slipping along a horizontal floor as shown in figure. P is a dot pointed on the rim of the wheel. At time ${t_1}$, P is at the point of contact between the wheel and the floor. At a later time ${t_2}$, the wheel has rolled, through one-half of a revolution. What is the displacement of P during this interval?

A. $90\,{\text{cm}}$
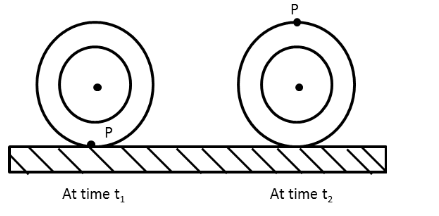
B. $168\,{\text{cm}}$
C. $40\,{\text{cm}}$
D. Data insufficient

Answer 1

Calculate the horizontal and vertical displacements of point P. Then calculate the resultant displacement of the point P.

Formulae used:
The circumference $C$ of the circle is given by
$\Rightarrow C = 2\pi r$ …… (1)
Here, $r$ is the radius of the circle.
The resultant displacement $s$ is given by
$\Rightarrow s = \sqrt {s_x^2 + s_y^2}$ …… (2)
Here, ${s_x}$ is the horizontal component of displacement and ${s_y}$ is the vertical component of displacement.

Complete step by step answer:
Calculate the horizontal displacement of the point P between the times ${t_1}$ to ${t_2}$.
The horizontal displacement ${s_x}$ of the point P is equal to half of the circumference $C$ of the wheel.
$\Rightarrow {s_x} = \dfrac{C}{2}$
Substitute $2\pi r$ for $C$ in the above equation.
$\Rightarrow {s_x} = \dfrac{{2\pi r}}{2}$
Substitute $3.14$ for $\pi$ and $45\,{\text{cm}}$ for $r$ in the above equation.
${s_x} = \dfrac{{2\left( {3.14} \right)\left( {45\,{\text{cm}}} \right)}}{2}$
$\Rightarrow {s_x} = 141.3\,{\text{cm}}$
Hence, the horizontal displacement of the point P is $141.3\,{\text{cm}}$.
Calculate the vertical displacement of the point P between the times ${t_1}$ to ${t_2}$.
The vertical displacement ${s_y}$ of the point P is equal to the diameter of the wheel which is twice the radius $r$ of the wheel.
$\Rightarrow {s_y} = 2r$
Substitute $45\,{\text{cm}}$ for $r$ in the above equation.
$\Rightarrow {s_y} = 2\left( {45\,{\text{cm}}} \right)$
$\Rightarrow {s_y} = 90\,{\text{cm}}$
Hence, the vertical displacement of the point P is $90\,{\text{cm}}$.
Now calculate the resultant displacement $s$ of the point P.
Substitute $141.3\,{\text{cm}}$ for ${s_x}$ and $90\,{\text{cm}}$ for ${s_y}$ in equation (2).
$\Rightarrow s = \sqrt {{{\left( {141.3\,{\text{cm}}} \right)}^2} + {{\left( {90\,{\text{cm}}} \right)}^2}}$
$\Rightarrow s = 167.5\,{\text{cm}}$
$\Rightarrow s = 168\,{\text{cm}}$
Therefore, the displacement of the point P is $168\,{\text{cm}}$.
Hence, the correct option is B.

Note: One may directly determine the diameter of the wheel to calculate the displacement of point P. But it is the vertical displacement and not the resultant displacement.