Question

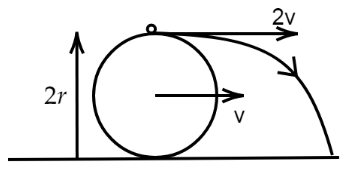
A wheel of radius $r$rolls without slipping on the ground, with speed $v$. When it is at a point $P$, a piece of mud flies off tangentially from its highest point, lands on the ground at point $Q$. Find the distance P Q ?

Answer 1

The path of the piece of mud follows a path of projectile motion. Find the horizontal velocity of the piece of mud and calculate the time of flight to calculate the distance of PQ.

Formula used:
The displacement of a particle in one dimensional motion is given by,
$s = ut + \dfrac{1}{2}a{t^2}$
where, $s$ is the displacement of the particle $u$ is the initial velocity of the particle $t$ is the time and $a$ is the acceleration of the particle.
The velocity of a body, moving with a velocity while rolling is,
${V_{rot}} = {V_{cm}} + \omega \times r$
where, ${V_{rot}}$ is the velocity with respect to the origin, ${V_{cm}}$ is the velocity with respect to the centre of mass and $r$ is the radius of the body and $\omega$ is angular velocity.

Complete step by step answer:
Since the body is moving while rolling so the speed of the piece of mud will be,
${V_{rot}} = {V_{cm}} + \omega \times r$
Here, we have given, ${V_{cm}} = v$and since the radius of the wheel is $r$ so, $\omega \times r$must be equal to $v$. So,
${V_{rot}} = v + v = 2v$.
Now, the piece of mud drops from a height of $r + r = 2r$. So, the time of flight is equal to time taken to drop from the height $2r$.

Hence, we can write for the vertical motion of piece of mud,
$s = ut + \dfrac{1}{2}a{t^2}$
$\Rightarrow 2r = 0 + \dfrac{1}{2}g{t^2}$
Up on simplifying we have, $t = \sqrt {\dfrac{{4r}}{g}}$
Now, the distance covered horizontally must be equal to the product of velocity and time of flight since the horizontal velocity does not change with time. Hence, the distance $PQ$ will be equal to,
$d = (2v)t$
Putting the value of time $t$ we have,
$d = 2v\sqrt {\dfrac{{4r}}{g}}$
$\therefore d = 4v\sqrt {\dfrac{r}{g}}$

Hence, distance between the points P and Q is $4v\sqrt {\dfrac{r}{g}}$.

Note: The piece of mud only travels the path of a half projectile. The path of the piece of mud is similar to when a stone or something is thrown horizontally from a height.For, a projectile motion time of flight is equal to, $\dfrac{{2u\sin \theta }}{g}$ where $u\sin \theta$ is vertical component of the velocity of the particle.