Question

A wheel of radius R is trapped in a mud pit and spinning. As the wheel is spinning. It splashes mud blobs with initial speed up from various points on its circumference. The maximum height from the centre of the wheel, to which a mud blob can reach, is:
A) $\dfrac{{{u^2}}}{{2g}}$.
B) $\dfrac{{{u^2}}}{{2g}} + \dfrac{{g{R^2}}}{{2{u^2}}}$.
C) $\dfrac{{{u^2}}}{g}$.
D) $R + \dfrac{{{u^2}}}{{2g}}$.

Answer 1

Projectile motion is defined as the motion in which the initial velocity of an object is at some angle from the horizontal and the motion of the object is in two dimensions. Maximum height during projectile motion is that vertical height where the vertical velocity of the object is zero.

Formula used: The formula of the maximum height for the projectile motion is given by,
$\Rightarrow H = \dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}}$
Where maximum height is $H$, the initial velocity is u, the angle from the horizontal is $\theta$.

Complete step by step answer:
It is given in the problem that a wheel of radius R is trapped in a mud pit and spinning as the wheel is spinning it splashes mud blobs with initial speed u from various points on its circumference and we need to find the maximum height to which the mud bob can reach from the centre of the wheel.

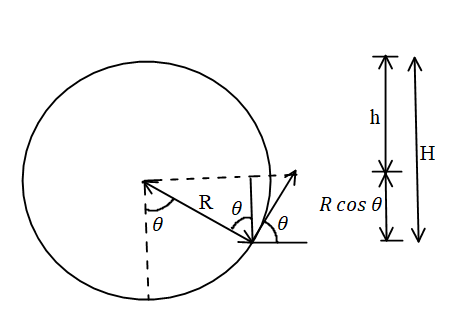
From the figure,
$\Rightarrow h = H - R\cos \theta$
It is mentioned in the problem that the maximum height has to be found out from the centre of the wheel.
$\Rightarrow {h_{\max }} = H - R\cos \theta$………eq. (1)
The formula of the maximum height for the projectile motion is given by,
$\Rightarrow H = \dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}}$………eq. (2)
Where maximum height is$H$, the initial velocity is u, the angle from the horizontal is$\theta$.
Replacing value of H from equation (2) into equation (1) we get,
$\Rightarrow {h_{\max }} = H - R\cos \theta$
$\Rightarrow {h_{\max }} = \left( {\dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}}} \right) - R\cos \theta$………eq. (3)
Applying the differentiation of equation (1) with respect to time and equating to zero for maximum height we get,
$\Rightarrow \dfrac{{d{h_{\max .}}}}{{d\theta }} = 0$
Replace the value of ${h_{\max }}$ from equation (1) we get,
$\Rightarrow \dfrac{{d{h_{\max .}}}}{{d\theta }} = 0$
$\Rightarrow \dfrac{{d\left[ {\left( {\dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}}} \right) - R\cos \theta } \right]}}{{d\theta }} = 0$
$\Rightarrow \dfrac{{{u^2}}}{{2g}} \cdot \left( {2\sin \theta \cdot \cos \theta } \right) + R \cdot \sin \theta = 0$
$\Rightarrow \left( {\dfrac{{{u^2}}}{g}} \right) \cdot \left( {\cos \theta } \right) + R = 0$
$\Rightarrow \left( {\dfrac{{{u^2}}}{g}} \right) \cdot \left( {\cos \theta } \right) = - R$
$\Rightarrow \cos \theta = \dfrac{{ - R \cdot g}}{{{u^2}}}$………eq. (4)
Since, ${\sin ^2}\theta = 1 - {\cos ^2}\theta$
Replacing value of $\cos \theta$ from equation (4) to equation (3) we get,
$\Rightarrow {h_{\max }} = \left( {\dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}}} \right) - R\left( {\dfrac{{ - R \cdot g}}{{{u^2}}}} \right)$
Since, ${\sin ^2}\theta = 1 - {\cos ^2}\theta$
\Rightarrow {h_{\max }} = \left\\{ {\dfrac{{{u^2}\left[ {1 - {{\left( {\dfrac{{ - R \cdot g}}{{{u^2}}}} \right)}^2}} \right]}}{{2g}}} \right\\} - R\left( {\dfrac{{ - R \cdot g}}{{{u^2}}}} \right)
$\Rightarrow {h_{\max }} = \dfrac{{{u^2}}}{{2g}}\left[ {1 - \dfrac{{{g^2}{R^2}}}{{{u^4}}}} \right] + \dfrac{{{R^2}g}}{{{u^2}}}$
$\Rightarrow {h_{\max }} = \dfrac{{{u^2}}}{{2g}} - \dfrac{{g{R^2}}}{{2{u^2}}} + \dfrac{{{R^2}g}}{{{u^2}}}$
$\Rightarrow {h_{\max }} = \dfrac{{{u^2}}}{{2g}} + \dfrac{{{R^2}g}}{{{u^2}}} - \dfrac{{g{R^2}}}{{2{u^2}}}$
$\Rightarrow {h_{\max }} = \dfrac{{{u^2}}}{{2g}} + \dfrac{{2{R^2}g - {R^2}g}}{{2{u^2}}}$
$\Rightarrow {h_{\max }} = \dfrac{{{u^2}}}{{2g}} + \dfrac{{{R^2}g}}{{2{u^2}}}$.
The maximum height is equal to${h_{\max }} = \dfrac{{{u^2}}}{{2g}} + \dfrac{{{R^2}g}}{{2{u^2}}}$.

The correct answer for this problem is option B.

Note: The students should understand and remember the formula of the maximum height in the projectile motion as it is helpful in solving problems like these. The differentiation of the maximum height with respect to the angle $\theta$ is done in order to find the angle at which the maximum height could be reached.