Question

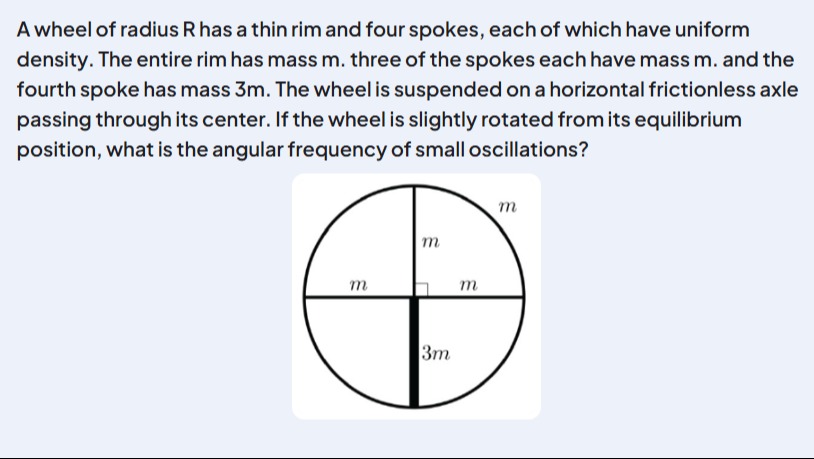
A wheel of radius R has a thin rim and four spokes, each of which have uniform density. The entire rim has mass m. three of the spokes each have mass m. and the fourth spoke has mass 3m. The wheel is suspended on a horizontal frictionless axle passing through its center. If the wheel is slightly rotated from its equilibrium position, what is the angular frequency of small oscillations?

Answer 1

$\omega = \sqrt{\frac{g}{3R}}$

Answer 2

Here's how to determine the angular frequency of small oscillations:

1. Find the center-of-mass displacement (d):

   • Rim: Mass = $m$, its center is at the geometric center.

   • Spokes: Each spoke has its center of mass at a distance $\frac{R}{2}$ from the center.

     • Three spokes (each with mass $m$) at angles $90^\circ$, $0^\circ$, and $180^\circ$ give:

       Their vertical contributions:

       $$m\left(\frac{R}{2}\right) \quad \text{(only the spoke at }90^\circ\text{ gives }+\frac{R}{2}\text{, the others give 0)}$$

     • The heavy spoke (mass $3m$) is vertical downward so its center is at

       vertical contribution:

       $$-3m\left(\frac{R}{2}\right).$$

   • Net vertical moment:

     $$m\left(\frac{R}{2}\right) - 3m\left(\frac{R}{2}\right)= -mR.$$

   • Total mass:

     $$M = m\ (\text{rim}) + (3m+ m+ m+ m)\ (\text{spokes})= 7m.$$

   • Displacement of center of mass:

     $$d = \frac{-mR}{7m} = -\frac{R}{7} \quad \Rightarrow \quad |d|=\frac{R}{7}.$$

2. Determine the moment of inertia (I) about the axle through the center:

   • Rim: $I_\text{rim} = mR^2.$

   • Each spoke: Is a thin rod of length $R$ about one end:

     $$I_\text{spoke} = \frac{1}{3}mR^2.$$
     • For three spokes (each $m$): total contribution = $$3\left(\frac{1}{3}mR^2\right) = mR^2.$$
     • For the heavy spoke (mass $3m$): $$I = \frac{1}{3}(3m)R^2 = mR^2.$$

   • Total Moment of Inertia:

     $$I = I_\text{rim} + I_\text{spokes} = mR^2 + mR^2 + mR^2 = 3mR^2.$$

3. Apply the physical pendulum formula:

   For small oscillations, the angular frequency is given by

   $$\omega=\sqrt{\frac{Mg\,d}{I}},$$

   where $d$ is the distance from the pivot to the center of mass.

   Substitute:

   $$Mg\,d = 7m\,g \left(\frac{R}{7}\right) = m\,g\,R.$$

   Thus,

   $$\omega = \sqrt{\frac{m\,g\,R}{3mR^2}} = \sqrt{\frac{g}{3R}}.$$

Summary:

• The center of mass is shifted downward by $\frac{R}{7}$.
• Total moment of inertia about the center is $I = 3mR^2$.
• Using $\omega = \sqrt{\frac{Mg\,d}{I}}$ gives $\omega = \sqrt{\frac{g}{3R}}$.