Question

A) What is the moment of inertia of a uniform circular disc of radius R and mass M about an axis passing through its center and normal to the disc? Also, show that the moment of inertia about any diameter of the disc is $\dfrac{1}{4}\text{M}{R^2}$.
B) State any two conditions for the formation of standing waves.

Answer 1

Moment of inertia is defined as the quantity that determines the torque needed for the desired angular acceleration about a rotational axis. Moment of inertia depends on the mass and axis of the object. Here, we compare the value of the moment of inertia in different axes and get the result.
Formula used:
$I = {I_c} + M{h^2}$

Complete step-by-step solution:

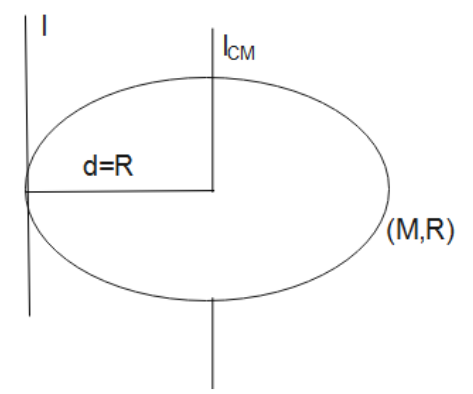
A). We know, the moment of inertia of a uniform circular disc about an axis through its center and perpendicular to its plane is given by:
${I_c} = \dfrac{1}{2}M{R^2}$
By the parallel axis theorem, the moment of inertia of a uniform circular disc about an axis touching the disc at its diameter and also normal to the disc is I.
Here, I is given by:
\eqalign{ & I = {I_c} + M{h^2} \cr &\Rightarrow I = \dfrac{1}{2}M{R^2} + M{R^2} \cr & \therefore I = \dfrac{3}{2}M{R^2} \cr}
Therefore, the moment of inertia of a uniform circular disc of radius R and mass M about an axis passing through its center and normal to the disc is given by 3/2MR2.
Also, from above we know that the moment of inertia of the disc is the same about any diameter.
Since,
\eqalign{ & {I_z} = {I_x} + {I_y} \cr &\Rightarrow {I_x} = {I_y} \cr &\Rightarrow {I_x} = 2{I_x} \cr &\Rightarrow {I_z} = \dfrac{{M{R^2}}}{2} \cr & \therefore {I_x} = \dfrac{{{I_z}}}{2} = \dfrac{{M{R^2}}}{4} \cr}
Thus, the moment of inertia of a disc about any of its diameter is given by the above equation.
B) The two conditions for the formation of standing waves are:

1. The two waves must be traveling in the same medium but in opposite directions.
2. They must have the same amplitude and frequency.

Additional information:
Moment of inertia is defined as the quantity that determines the torque needed for the desired angular acceleration about a rotational axis. Its S.I unit is kg $m^2$.
Standing waves also known as stationary waves. It is a wave, which oscillates in time but whose peak amplitude profile does not move in space.

Note: Moment of inertia depends on mass distribution of object and the axis is chosen, with larger moments is required the more torque to change the object’s rate of rotation. It is an extensive property. For a point mass, the moment of inertia is simply the mass times the square of the perpendicular distance to the axis of rotation.