Solveeit Logo
Login

Question

Question: A) What is the expansion formula for \[{(a - b)^2}\] B) Expand \[{(x - 3)^3}\] C) In rectangle ...

A) What is the expansion formula for (a−b)2{(a - b)^2}
B) Expand (x−3)3{(x - 3)^3}
C) In rectangle ABCD, If l(AB)=8cml\left( {AB} \right) = 8cm, l(BC)=6cml\left( {BC} \right) = 6cm then find l(CD)&l(AC)l\left( {CD} \right)\& l\left( {AC} \right)
D) What are the factors of x2−16{x^2} - 16

Explanation

Solution

The Binomial Theorem states that, where n is a positive integer,
(x+y)n=∑k=0nnCkxn−kyk=xn+nC1xn−1y+nC2xn−2y2+......{(x + y)^n} = \sum\limits_{k = 0}^n {n{C_k}{x^{n - k}}{y^k}} = {x^n} + n{C_1}{x^{n - 1}}y + n{C_2}{x^{n - 2}}{y^2} + ......
Formula used- nCr=n!r!(n−r)!n{C_r} = \dfrac{{n!}}{{r!\left( {n - r} \right)!}}

Complete step-by-step answer:
a) We have to find the expansion formula for (a−b)2{(a - b)^2}
(a−b)2=(a−b)(a−b){(a - b)^2} = (a - b)(a - b)
Multiply the two factors we have,
=a2−ab−ab+b2= {a^2} - ab - ab + {b^2}
Simplifying the above equation,
=a2−2ab+b2= {a^2} - 2ab + {b^2}
Hence, the expansion formula for (a−b)2{(a - b)^2}is a2−2ab+b2{a^2} - 2ab + {b^2}.

b) We have to Expand (x−3)3{(x - 3)^3}
From Binomial theorem we have,
(x+y)n=∑k=0nnCkxn−kyk=xn+nC1xn−1y+nC2xn−2y2+......{(x + y)^n} = \sum\limits_{k = 0}^n {n{C_k}{x^{n - k}}{y^k}} = {x^n} + n{C_1}{x^{n - 1}}y + n{C_2}{x^{n - 2}}{y^2} + ......
Putting y=-3 and apply binomial theorem to get the expansion of (x−3)3{(x - 3)^3} x+(−3)3=∑k=033Ckx3−k(−3)k{\\{ x + ( - 3)\\} ^3} = \sum\limits_{k = 0}^3 {3{C_k}{x^{3 - k}}{{( - 3)}^k}}
=x3+3C1x3−1(−3)+3C2x3−2(−3)2+3C3x3−3(−3)3= {x^3} + 3{C_1}{x^{3 - 1}}( - 3) + 3{C_2}{x^{3 - 2}}{( - 3)^2} + 3{C_3}{x^{3 - 3}}{( - 3)^3}
Using the formula we mention in hint nCr=n!r!(n−r)!n{C_r} = \dfrac{{n!}}{{r!\left( {n - r} \right)!}},
=x3−3!1!(3−1)!3x2+3!2!(3−2)!9x−3!3!×27= {x^3} - \dfrac{{3!}}{{1!(3 - 1)!}}3{x^2} + \dfrac{{3!}}{{2!(3 - 2)!}}9x - \dfrac{{3!}}{{3!}} \times 27
Simplifying that,
=x3−3×2×12×13x2+3×2×12×19x−27= {x^3} - \dfrac{{3 \times 2 \times 1}}{{2 \times 1}}3{x^2} + \dfrac{{3 \times 2 \times 1}}{{2 \times 1}}9x - 27
Multiply and divide the terms, we get,
=x3−9x2+27x−27= {x^3} - 9{x^2} + 27x - 27
Hence expanding (x−3)3{(x - 3)^3} we get,
x3−9x2+27x−27{x^3} - 9{x^2} + 27x - 27

c) In rectangle ABCD, If l(AB)=8cml\left( {AB} \right) = 8cm, l(BC)=6cml\left( {BC} \right) = 6cm then find l(CD)&l(AC)l\left( {CD} \right)\& l\left( {AC} \right)
We have to find out, l(CD)&l(AC)l\left( {CD} \right)\& l\left( {AC} \right)

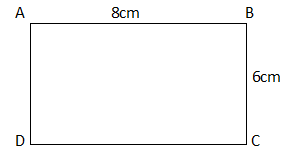
For a rectangle the opposite sides are of the same length.
Therefore, AB = CD, BC = DAAB{\text{ }} = {\text{ }}CD,{\text{ }}BC{\text{ }} = {\text{ }}DA
The measure of sides,

{l\left( {AB} \right) = 8cm,{\text{ }}l\left( {BC} \right) = 6cm} \\\ {{\text{So}},{\text{ }}l\left( {AB} \right) = l\left( {CD} \right) = 8cm} \end{array}$$ Thus, $$l\left( {CD} \right) = 8cm$$. The diagonal is AC, since ABCD is a rectangle so the angles are right angle. Applying Pythagoras theorem, $$A{C^2} = A{B^2} + B{C^2}$$ Substituting the values, $$AC = \sqrt {{8^2} + {6^2}} $$ $$ = \sqrt {64 + 36} $$ = \sqrt {100} \\\ = 10{\text{ cm}} \\\ Then the length of AC is 10cm. $$l\left( {AC} \right) = 10cm.$$ D) We have to find out the factor of $${x^2} - 16$$ Applying the formula, $${a^2} - {b^2} = (a + b)(a - b)$$ Using the above formula, $${x^2} - 16$$$$ = {x^2} - {4^2}$$ $$ = (x + 4)(x - 4)$$ So the factors are $$\left( {x + 4} \right){\text{ and }}\left( {x - 4} \right)$$ **Note:** A combination is a grouping or subset of items. For a combination, $$C(n,r){ = ^n}{C_r} = \dfrac{{n!}}{{(n - r)!r!}}$$ Where, factorial n is denoted by $$n!$$and defined by $$n! = n\left( {n - 1} \right)\left( {n - 2} \right)\left( {n - 3} \right)\left( {n - 4} \right) \ldots \ldots .2.1$$