Question

(a) What are coherent sources of light? State two conditions for two light sources to be coherent.
(b) Derive a mathematical expression for the width of the interference fringes obtained in Young’s double slit experiment with the help of a suitable diagram.
(c) If $s$ is the size of the source and $b$ its distance from the plane of the two slits, what should be the criterion for the interference fringes to be seen?

Answer 1

Try to visualize the diagram and use different approximations to solve the question. General geometry can be used. The observations of Young’s double-slit experiment will give a perspective about the occurrence of interference. Coherency is the key to implement the experiment successfully.

Complete step by step answer:
(a) When two light sources produce waves having the same frequency and have a constant phase difference with time, they are called to be coherent. The two conditions for two light sources to be coherent are as follows:
-The coherent sources of light must have originated from a single source and must be monochromatic (that is they have a single wavelength) in nature.
-The path difference between the light waves from the two sources must be small.

(b) Let, a monochromatic source of light with wavelength $\lambda$ is used to illuminate a narrow slit, $S$ therefore producing two coherent sources of light through the two slits ${S_1}$ and${S_2}$.

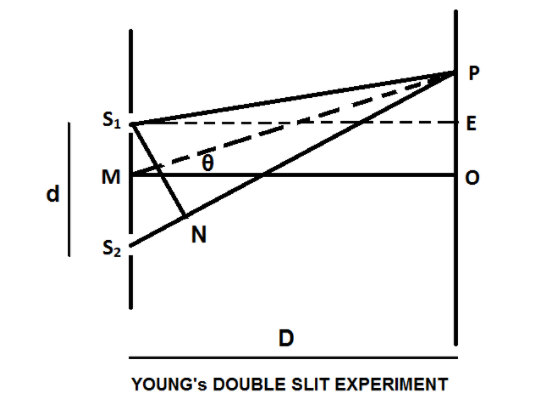
Now, the light waves from the slits ${S_1}$ and${S_2}$ superimpose with each other and reach point $P$ as shown in the figure and have a path difference of${S_2}P - {S_1}P$.
Let $d =$ the separation between the slits, $D =$ the distance between the screen and the slits, $x =$ the distance between the centre of the screen to point $P$ and $\theta =$ the angle between $MP$ and $MO$. Now, draw a perpendicular,${S_1}N$ on line ${S_2}P$ such that distances $P{S_1}$ and $PN$ are equal. Therefore, the path difference is${S_2}N$. Let, the point $P$ be at a distance $x$ from $O$. Therefore,
$PE = x - \dfrac{d}{2}$ and $PF = x + \dfrac{d}{2}$ .

Consider the right-angled triangles in the figure, we get:
$\Rightarrow {\left( {{S_2}P} \right)^2} - {\left( {{S_1}P} \right)^2} = \left[ {{D^2} + {{\left( {x + \dfrac{d}{2}} \right)}^2}} \right] - \left[ {{D^2} + {{\left( {x - \dfrac{d}{2}} \right)}^2}} \right]$
Simplify the equation:
$\Rightarrow \,{\left( {{S_2}P} \right)^2} - {\left( {{S_1}P} \right)^2} = 2xd$
$\Rightarrow \left( {{S_2}P + {S_1}P} \right)\left( {{S_2}P - {S_1}P} \right) = 2xd$
$\, \Rightarrow {S_2}P - {S_1}P = \dfrac{{2xd}}{{{S_2}P + {S_1}P}}$

Approximate that,
$\Rightarrow {S_2}P \cong {S_1}P \cong D$
So, Path difference $= {S_2}P - {S_1}P = \dfrac{{xd}}{D}$
The condition for bright fringe at point P on the screen is:
$\Rightarrow \,\,{S_2}P - {S_1}P = m\lambda$
$\Rightarrow \,\dfrac{{xd}}{D} = m\lambda$
The condition for dark fringe at point P on the screen is:
$\Rightarrow \,\,{S_2}P - {S_1}P = \left( {2m + 1} \right)\dfrac{\lambda }{2}$
$\Rightarrow \,\dfrac{{xd}}{D} = \left( {2m + 1} \right)\dfrac{\lambda }{2}$
Where $m$ is the order of the fringe and $\lambda$ is the wavelength.

In order to find the fringe width, $\beta$ subtract the distance of the two consecutive bright or dark fringes.The fringe of ${m^{th}}$ order will be seen at:
${x_m} = \dfrac{{m\lambda D}}{d}$
The fringe of ${\left( {m + 1} \right)^{th}}$ order will be seen at:
${x_{m + 1}} = \dfrac{{\left( {m + 1} \right)\lambda D}}{d}$
So, the fringe width,$\beta$ is given by:
$\Rightarrow \,\beta = {x_{m + 1}} - {x_m}$
$\therefore \beta = \dfrac{{\lambda D}}{d}$

(c) If $s$ is the size of the source and $b$ its distance from the plane of the two slits, then the criterion for the interference fringes to occur is:
$\dfrac{s}{b} < \dfrac{\lambda }{d}$
Where $d =$ the separation between the slits and $\lambda =$ wavelength of the monochromatic light.Also, the size of the source and the distance between the slits should be small.

Note: The fringe width for both the bright and dark fringes will be the same. This is because air is present between the slits and the screen and thus acting as a parallel film. Therefore, the light will not deviate from its original path and produce fringes of equal widths. If a Plano-convex lens is used to produce interference then circular fringes will occur as the air film will be of variable thickness.