Solveeit Logo
Login

Question

Question: A weightless spring of length \(60cm\) and force constant \(100N{{m}^{-1}}\) is kept straight and un...

A weightless spring of length 60cm60cm and force constant 100Nm−1100N{{m}^{-1}} is kept straight and unstretched on a smooth horizontal table and its ends are rigidly fixed. A mass of 0.25kg0.25kg is attached at the middle of the spring and is slightly displaced along the length. The time period of the oscillation of the mass will be:
A.π20s B.π10s C.π5s D.π200s \begin{aligned} & A.\dfrac{\pi }{20}s \\\ & B.\dfrac{\pi }{10}s \\\ & C.\dfrac{\pi }{5}s \\\ & D.\dfrac{\pi }{\sqrt{200}}s \\\ \end{aligned}

Explanation

Solution

First of all the equivalent spring constant of both mass and the spring should be found. Then calculate the time period of oscillation using the given values in the question. These all will help you in solving the question.

Complete step by step answer:

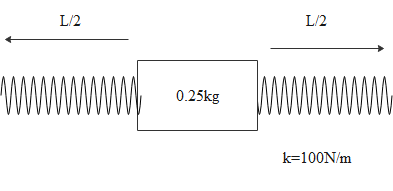
In order to solve this problem we have to get to know the equivalent spring constant of the whole system. When we look at the figure, we get to know that the system is similar to the parallel combination of the springs in general.
Therefore the equivalent spring constant will be,
keqvlnt⁡=k1+k2{{k}_{eqv\operatorname{lnt}}}={{k}_{1}}+{{k}_{2}}
As the length of a spring is inversely proportional to the spring constant, here we can see that the mass is added at the middle of spring. That is the length of becoming half of the previous one. So the spring constant will be double of the original one.
Therefore,
k=2×100=200Nm−1k=2\times 100=200N{{m}^{-1}} keqvlnt⁡=k1+k2=400{{k}_{eqv\operatorname{lnt}}}={{k}_{1}}+{{k}_{2}}=400
Substituting the values in it will give,
keqvlnt⁡=k1+k2=400{{k}_{eqv\operatorname{lnt}}}={{k}_{1}}+{{k}_{2}}=400
Therefore we can now find the time period of oscillation of the particle,
The equation of time period of oscillation is given as,
T=2πmkeqvlnt⁡T=2\pi \sqrt{\dfrac{m}{{{k}_{eqv\operatorname{lnt}}}}}
Substituting the values in it,
T=2π0.25400 =π20s \begin{aligned} & T=2\pi \sqrt{\dfrac{0.25}{400}} \\\ & =\dfrac{\pi }{20}s \\\ \end{aligned}
Therefore the time period oscillation has been found out. The correct answer is option A.

Note:
A stronger spring-with a higher value of k will be moving with the equivalent mass more quickly for a comparatively small period of time. As the spring constant k gets increases, the time period gets decreased. For a certain mass, which means a higher acceleration so the mass will be moving faster and can complete its motion faster.