Question

A weightless rod of length $2l$ carries two equal masses $m$ one second at lower end $A$ and the other at the middle of the rod at $B$ . The rod can rotate in a vertical plane about a fixed horizontal axis passing through $C$ . What horizontal velocity must be imparted to the mass at $A$ so that it just completes the vertical circle.
A. $\sqrt {\dfrac{{48}}{5}gl}$
B. $\sqrt {\dfrac{{45}}{5}gl}$
C. $\sqrt {\dfrac{{40}}{5}gl}$
D. $\sqrt {\dfrac{{35}}{5}gl}$

Answer 1

In this question first we will find the potential energy and then kinetic energy and then we will apply law of conservation of energy and then compare to get the horizontal velocity that must be imparted to the mass at $A$ so that it just completes the vertical circle.

Formula used:
$K.E. = \dfrac{1}{2}m{v^2}$
Where,
$m$ is the mass and
$v$ is the velocity.
$P.E = mgh$
$g$ is the acceleration due to gravity and
$h$ is the height.

Complete step by step solution:

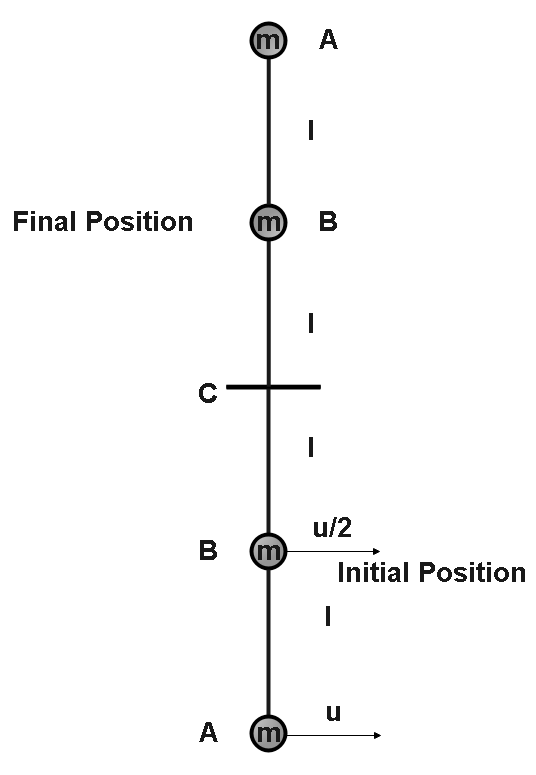
Given,
Length of the rod is $2l$
And mass is given $m$
Let the initial velocity given to the mass at A be $u$
Then, the velocity of mass at B is $\dfrac{u}{2}$
As the system moves from initial position to final position.
Then, there is an increase in potential energy
And that is
$P.{E_{total}} = {(mgh)_A} + {(mgh)_B}$
Now substituting the value, we get,
$P.{E_{total}} = mg4l + mg2l \\\ P.{E_{total}} = 6mgl \\\$
We know that from law of conservation of energy potential energy is equal to kinetic energy
So,

$$6mgl = \dfrac{{mv_B^2}}{2} + \dfrac{{mv_A^2}}{2} \\\ \Rightarrow 6mgl = \dfrac{1}{2}m{\left( {\dfrac{u}{2}} \right)^2} + \dfrac{1}{2}m{u^2} \\\$$

Where, velocity of mass at B is $\dfrac{u}{2}$ substituting and further solving the equation,

$$\Rightarrow 6mgl = \dfrac{1}{8}m{u^2} + \dfrac{1}{2}m{u^2} \\\ \Rightarrow 6mgl = \dfrac{5}{8}m{u^2} \\\$$

Now, cross multiplying to find $u$

$$\Rightarrow {u^2} = \dfrac{{48}}{5}lg \\\ \Rightarrow u = \sqrt {\dfrac{{48}}{5}gl} \\\$$

So, the horizontal velocity must be imparted to the mass at $A$ so that it just completes the vertical circle $\sqrt {\dfrac{{48}}{5}gl}$
Hence, the correct option is A.

Note:
The potential energy of point A is ${(mgh)_A} = 4mgl$ because if we see in the diagram that the distance between final and initial position is $4l$ so we have put $h$ as $4l$ .You must remember the conservation of energy to solve this question.