Question

A weightless ladder, 20 ft long rests against a frictionless wall at an angle of 60⁰ with the horizontal. A 150 pound man is 4 ft from the top of the ladder. A horizontal force is needed to prevent it from slipping. Choose the correct magnitude from the following

• A. 175 lb
• B. 100 lb
• C. 70 lb
• D. 150 lb

Answer 1

Answer: (C)

70 lb

Answer 2

Since the system is in equilibrium therefore $\sum_{}^{}{F_{x} = 0}$and $\sum_{}^{}{F_{y} = 0}$ $\mathbf{\therefore}$ $\mathbf{F =}\mathbf{R}_{\mathbf{2}}$and $\mathbf{W =}\mathbf{R}_{\mathbf{1}}$

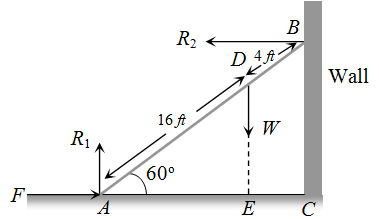
Now by taking the moment of forces about point B.

$F . ( B C ) + W . ( E C ) =$ $R_{1}(AC)$

[from the figure EC= 4 cos 60]

$F.(20\sin 60) + W(4\cos 60) = R_{1}(20\cos 60)10\sqrt{3}F + 2W = 10R_{1}$ $\left\lbrack \text{As}R_{1} = W \right\rbrack$

∴$F = \frac{8W}{10\sqrt{3}} = \frac{8 \times 150}{10\sqrt{3}} = 70lb$