Question
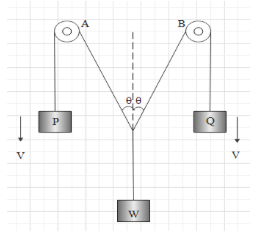
Question: A weight W is tied to two strings passing over the frictionless pulleys A and B as shown in the figu...
A weight W is tied to two strings passing over the frictionless pulleys A and B as shown in the figure. If weights P and Q move downwards with speed V, the weight W at any instant rises with the speed:
A. Vcosθ
B. 2Vcosθ
C. cosθV
D. cosθ2V
Solution
Hint- In the given figure we can consider a right triangle connecting one of the pulleys, the midpoint of line joining the two pulleys and point of suspension of weight W. Using Pythagoras theorem, we will get an equation relating length of the string and height to which weight can be raised. By differentiating this equation with respect to time we can find the velocity with which the weight moves upward.
Step by step solution:
It is given that a weight is tied to two strings passing over two frictionless pulleys. If weights P and Q move downwards with a speed V, the weight W Rises upward. We need to find the speed with which weight W rises upward.
Consider the triangle BOS shown in the figure below.
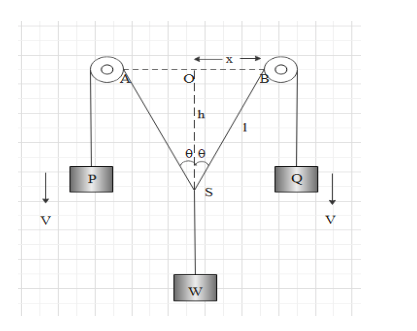
Since it is a right-angled triangle, we can use the Pythagoras theorem.
let the length of the string be l. Then we can write
l2=h2+x2
Let us differentiate this equation with respect to t.
⇒2ldtdl=2hdtdh+0..............(1)
We know that the rate of change of distance is velocity. Hence, we can write
dtdl=V
Substituting this in equation 1 we get
⇒2l×V=2hdtdh+0.................(2)
The rate of change of the height h will give us the velocity of the block upwards. Let this velocity be denoted as u.
⇒dtdh=u
Thus equation 2 becomes
⇒2lV=2hu
⇒u=hlV
⇒u=lhV
From the triangle BOS, we can find that the value of cosθ is given as
cosθ=hypotenuseadjacentside
⇒cosθ=lh
Thus, we can substitute cosθ instead of lh
Using this we get the value of velocity u as
∴u=cosθV
So, the correct option is option C.
Note: Remember that while taking the derivative of equation l2=h2+x2 , the derivative of x with respect to time will be zero. This is because the value of x is a constant. Its value does not change with time. So, its derivative with respect to time will be zero.
