Question

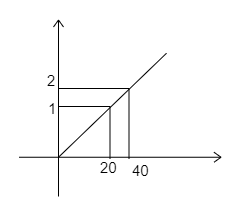
A weight $W$ is suspended through a rope of length $1\,m$ and cross sectional area ${10^{ - 6}}\,{m^2}$ from a rigid support. The relation between change in length of rope $\Delta l$ and $W$ is shown in the graph. The young’s modulus of elasticity is: (Change in length are in ${10^{ - 4}}$)

(A) $2 \times {10^{ - 5}}$
(B) $2 \times {10^{11}}$
(C) $5 \times {10^4}$
(D) $5 \times {10^{10}}$

Answer 1

Hint
The young modulus is determined by the relation of the stress and the strain of the object. The relation of the weight and the change in length is given in the graph by using that data, the young’s modulus of elasticity of the body is determined.
The Young’s modulus is given by,
$\Rightarrow Y = \dfrac{\sigma }{\varepsilon }$
Where, $Y$ is the young’s modulus and $\sigma$ is the stress and $\varepsilon$ is the strain.
The stress is given by,
$\Rightarrow \sigma = \dfrac{F}{A}$
Where, $\sigma$ is the stress, $F$ is the force of the object and $A$ is the cross sectional area of the object.
The strain is given by,
$\Rightarrow \varepsilon = \dfrac{{\Delta l}}{l}$
Where, $\varepsilon$ is the strain, $\Delta l$ is the changer in length and $l$ is the length.

Complete step by step answer
Given that, The length of the rope is, $l = 1\,m$
The cross sectional area is, $A = {10^{ - 6}}\,{m^2}$
Now, The Young’s modulus is given by,
$\Rightarrow Y = \dfrac{\sigma }{\varepsilon }\,.......................\left( 1 \right)$
By substituting the formula of the stress and the strain in the above equation (1), then the equation (1) is written as,
$\Rightarrow Y = \dfrac{{\left( {\dfrac{F}{A}} \right)}}{{\left( {\dfrac{{\Delta l}}{l}} \right)}}$
By rearranging the terms in the above equation, then the above equation is written as,
$\Rightarrow Y = \dfrac{{F \times l}}{{A \times \Delta l}}$
By substituting the area value and the length value in the above equation, then the above equation is written as,
$\Rightarrow Y = \dfrac{{F \times 1}}{{{{10}^{ - 6}} \times \Delta l}}$
The weight value and the change in length values are taken from the graph and substituted in the above equation, then,
$\Rightarrow Y = \dfrac{{20 \times 1}}{{{{10}^{ - 6}} \times 1 \times {{10}^{ - 4}}}}$
On further simplification, then the above equation is written as,
$\Rightarrow Y = \dfrac{{20}}{{{{10}^{ - 10}}}}$
By rearranging the terms in the above equation, then
$\Rightarrow Y = 20 \times {10^{10}}$
The above equation is also written as,
$\Rightarrow Y = 2 \times {10^{11}}\,N{m^{ - 2}}$
Hence, the option (B) is the correct answer.

Note
The Young's modulus value of the object is directly proportional to the stress of the object and inversely proportional to the strain of the object. If the stress increases the young’s modulus also increases. If the strain increases, the young’s modulus decreases.