Question
Question: A wedge of mass \[M\] with a spring of stiffness \(k\) is kept on a smooth horizontal surface. A rod...
A wedge of mass M with a spring of stiffness k is kept on a smooth horizontal surface. A rod of mass m is kept on the wedge as shown in the figure. The system is in equilibrium. Assuming that all surfaces are smooth, the potential energy stored in the spring is:
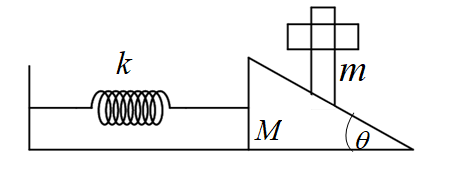
A. 2kmg2tan2θ
B. 2km2gtan2θ
C. 2km2g2tan2θ
D. km2g2tan2θ
Solution
In Physics, spring is a device used to store potential energy in the form of elastic energy. When we extend the spring by applying an external force on it, this force is stored inside it as mechanical energy, as soon as we withdraw the applied force spring regains its original position using the stored energy.
Complete step by step solution:
Let us first draw a free body diagram to show all the forces acting on the rod as shown in the figure.
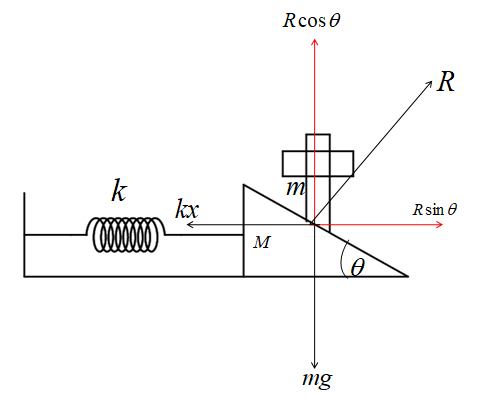
Now the system is in equilibrium it means, all the forces balance each other. From the figure, we can write these balancing forces.
mg=Rcosθ …………..(1)
kx=Rsinθ……………. (2)
Let us divide equation (2) by (1) and get the value of x.
mgkx=tanθ
⇒x=kmgtanθ …………………. (3)
The formula to calculate the potential energy stored in the spring is given below.
PE=21kx2
Let us now put the value of xfrom equation (3).
PE=21k(kmgtanθ)2
Let us further simplify it.
PE=2km2g2tan2θ
This is the potential energy stored in the spring when the system is in equilibrium.
Hence, the correct option is (C) 2km2g2tan2θ.
Note:
An equilibrium condition for this type of system is when all the forces cancel or balance each other. To know which force is balanced by which, we have to draw the free body diagram.
To draw a free body diagram, we have to resolve all the forces in their horizontal and vertical components
