Question

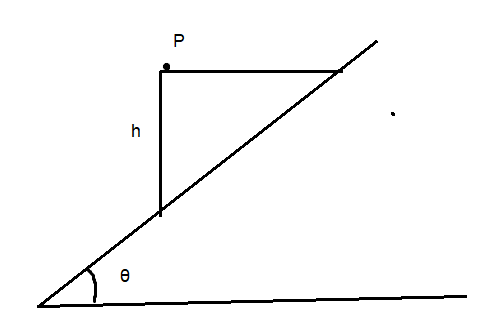
A wedge of height $h$ is released from rest with a light particle $P$ placed on it as shown. The wedge slides an incline which makes an angle $\theta$ with the horizontal. All the surfaces are smooth, find the time after which $P$ will reach the surface of the incline.

A.$\sqrt {\dfrac{{2h}}{{g{{\sin }^2}\theta }}}$
B.$\sqrt {\dfrac{h}{{g{{\sin }^2}\theta }}}$
C.$\sqrt {\dfrac{h}{{2g{{\sin }^2}\theta }}}$
D.$\sqrt {\dfrac{h}{{g{{\sin }^2}\theta }}}$

Answer 1

According to Newton’s first law of motion, a body tends to be at rest or in uniform motion along a straight line unless there is no external force acting on it. Whereas pseudo force is false force felt by an object due to acceleration and its tendency to be at rest (Newton's first law of motion). Use the equation of motion for the particle in terms of distance, initial velocity, time, and acceleration where the initial velocity for this case is zero. Also, the concept of slope is needed here.
Formula Used:
$s = ut + \dfrac{1}{2}a{t^2}$
$\tan \theta = \dfrac{h}{x}$

Complete answer:
According to the given statement,
Height of wedge = $h$
The angle of inclination = $\theta$
Friction force = $0$
Let the distance between Point $P$ and surface be $x$ as shown below.
i.e., the total distance traveled by particle from point $P$ to $x$ can also be expressed as
$\tan \theta = \dfrac{h}{x} \Rightarrow x = \dfrac{h}{{\tan \theta }}$ …… (1)
Now, since the wedge is sliding on a frictionless surface, the net acceleration is only because of gravitational force.

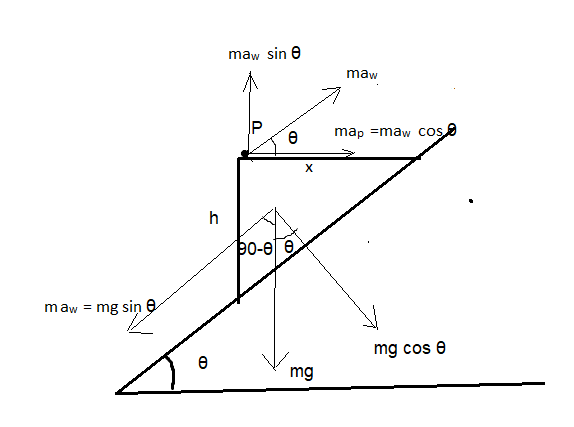
Hence according to the free body diagram, we can derive the following expression
Acceleration of wedge, ${a_w} = gsin{\text{ }}\theta$
Now since the particle is accelerated toward the inclined surface because of pseudo force the acceleration of the particle can be given as
${a_p} = {a_w}cos\theta = gsin\theta \times cos\theta ...........(2)$
Also, according to the third kinematic equation, the relation between the acceleration of particle (ap), time to reach the inclined surface (t), and distance traveled by a particle (x) is given as
$x = ut + \dfrac{1}{2}{a_p}{t^2}$
Here, u is the initial velocity. For our simplicity consider that initially both particles and wedges are at rest.
∴$x = \dfrac{1}{2}{a_p}{t^2}$
Whereas from statements 1 and 2 we get
i.e., $\dfrac{h}{{\tan \theta }} = \dfrac{1}{2}g\sin \theta \times \cos \theta \times {t^2}$
$\Rightarrow t = \sqrt {\dfrac{{2h}}{{\dfrac{{\sin \theta }}{{\cos \theta }} \times \sin \theta \times \cos \theta \times g}}}$
$\Rightarrow t = \sqrt {\dfrac{{2h}}{{{\text{g si}}{{\text{n}}^2}\theta }}}$

correct option is A.

Note:
For any free body diagram it's important to draw all forces acting on block, wedge, particle, etc., to understand the relationship between balance and unbalance force. Also, we must be careful about the frame of reference and external forces acting on a block, in this case since friction across all surfaces is zero, our problem becomes much easier to solve.
In case if there was some friction between the wedge and inclined surface the equation for this will be expressed as
$m{a_w} = mgsin\theta -f$
Here $f$ can be considered as a frictional force.