Question

A wave is travelling along a string. At an instant the shape of the string is as shown in the figure. At this instant, point A is moving upwards. Which of the following statements are correct?

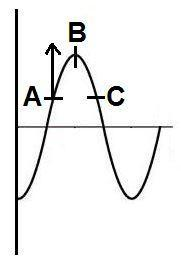
A. The wave is traveling to the right
B. Displacement amplitude of the wave is equal to the displacement of B at this instant.
C. At this instant velocity of C is also directed upwards
D. Phase difference between A and C may be equal to $\dfrac{\pi }{2}$

Answer 1

As the first step you could recall the relation between the particle velocity and wave velocity or else you could derive the same from the expression of displacement of a particle in a wave. Using this expression, you could find the direction of the wave velocity for option A and also particle velocity for option C and thereby see whether those statements are true or false. Amplitude is the maximum displacement, so find whether point B shows maximum displacement. Also, see whether point A and C are congruent points on a wave equidistant from the x-axis with the same velocity directed in the opposite direction.

Formula used:
Relation between particle velocity and wave velocity,
${{v}_{p}}=-{{v}_{w}}\dfrac{dy}{dx}$

Complete step-by-step answer:
In the question we are given a figure of a wave traveling along a string at an instant. It is also given that, at this particular instant, the point A is moving upwards. We are supposed to find which of the given options are true for the given wave.
Let us recall the expression for displacement of a wave,
$y=A\sin \left( \omega t-kx \right)$
This basically is the displacement of a particle at any instant t.
Where, A is the amplitude of the wave. Amplitude is the maximum displacement of the particle.
$\omega$ is the angular frequency, t is the time taken for the displacement and k is the wave number.
Particle velocity ${{v}_{p}}$ is given by,
${{v}_{p}}=\dfrac{dy}{dt}$
$\Rightarrow {{v}_{p}}=A\omega \cos \left( \omega t-kx \right)$ ……………………… (1)
Also,
$\dfrac{dy}{dx}=-Ak\cos \left( \omega t-kx \right)$ …………………………… (2)
From (1) and (2),
${{v}_{p}}=-\dfrac{\omega }{k}\dfrac{dy}{dx}$
Where, $\dfrac{\omega }{k}$ is the wave velocity$\left( {{v}_{w}} \right)$.
So we get the relation between particle and wave velocity as,
${{v}_{p}}=-{{v}_{w}}\dfrac{dy}{dx}$ ………………….. (3)
Now let us come back to the question.
At point A, the particle is moving upward and ${{v}_{p}}$ by convention is positive upward, also slope $\left( \dfrac{dy}{dx} \right)$ at that point is positive. Therefore, in order to satisfy equation (3) wave velocity ${{v}_{w}}$ should be negative. At point A wave velocity is negative, that is the wave is moving towards the left. So, option A is false.
Amplitude by definition is the maximum displacement. Maximum displacement of the given wave is clearly at point B. So, option B is found to be true.
At point C, just by looking at the given figure we can say that it is directed downward. But let us verify this using (3). We had found earlier that the wave velocity of the given wave is negative and also from the figure we can see that the slope $\left( \dfrac{dy}{dx} \right)$ is negative. Therefore, the particle velocity at point is negative, which indicates that at point C, the velocity is directed downward. So, option C is false.
From the diagram, points A and C are found to be equidistant from x-axis. That means the velocities at points A and C are the same but they are directed in the opposite direction. Hence, we could say that the phase difference between the two points is $\dfrac{\pi }{2}$ . So, option D is true.

So, the correct answers are “Option B and D”.

Note: In questions like this where statements are given for us to find whether they are true or not, chances are there for multiple correct answers. So, to be on the safe side, we could approach such questions in a step by step manner. That is, we should analyze every statement one by one and see whether they are true.