Question

A water tank standing on the floor has two small holes vertically one above another the other punched on one side. The holes are ${h_1}\,cm$ and ${h_2}\,cm$ above the floor. How high does water stand in the tank, when the jets from the holes hit the floor at the same point?
(A) $\left( {{h_2} - {h_1}} \right)$
(B) $\left( {{h_2} + {h_1}} \right)$
(C) $\left( {{h_2}^2 - {h_1}^2} \right)$
(D) $\dfrac{{{h_2}}}{{{h_2} - {h_1}}}$

Answer 1

In the problem, we have to determine the height of the water which stands in the tanks. By using Torricelli's theorem or Torricelli's equation of the range of the liquid formula, the height of the water inside the tank is determined.

Formulae Used:
By Torricelli’s equation, the range of the liquid is given as,
$R = \sqrt {4 \times \left( {H - h} \right)h}$
Where, $R$ is the range of the liquid or the distance from the tank to the water hits the ground, $H$ is the height of the water inside the tank, $h$ is the height of the holes from the floor.

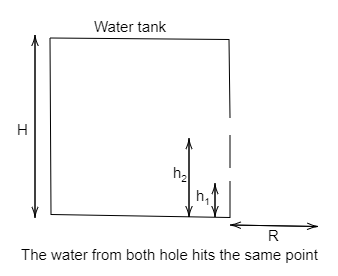
Complete step-by-step solution:
By Torricelli’s equation, the range of the liquid is given as,
For hole $1$,
${R_1} = \sqrt {4 \times \left( {H - {h_1}} \right){h_1}} \,...................\left( 1 \right)$
Where, ${R_1}$ is the range of the liquid for the first hole and ${h_1}$ is the height of the first hole from the floor.
By Torricelli’s equation, the range of the liquid is given as,
For hole $2$,
${R_2} = \sqrt {4 \times \left( {H - {h_2}} \right){h_2}} \,...................\left( 2 \right)$
Where, ${R_2}$ is the range of the liquid for the second hole and ${h_2}$ is the height of the second hole from the floor.
In the problem, it is given that the jets from the holes hit the floor at the same point, which means that the range of the liquid from both the holes are the same. Then,
${R_1} = {R_2}$
Now equating the equation (1) and equation (2), then
$\sqrt {4 \times \left( {H - {h_1}} \right){h_1}} = \sqrt {4 \times \left( {H - {h_2}} \right){h_2}}$
On both sides, taking the root for the term $4$, then
$2\sqrt {\left( {H - {h_1}} \right){h_1}} = 2\sqrt {\left( {H - {h_2}} \right){h_2}}$
By cancelling the same terms and the square root on both sides, then
$\left( {H - {h_1}} \right){h_1} = \left( {H - {h_2}} \right){h_2}$
Now multiplying the terms on both sides, then
$\left( {H{h_1} - {h_1}^2} \right) = \left( {H{h_2} - {h_2}^2} \right)$
By rearranging the terms in the above equation, then
$H{h_1} - H{h_2} = {h_1}^2 - {h_2}^2$
By taking the term $H$ as common in LHS, then
$H\left( {{h_1} - {h_2}} \right) = \left( {{h_1}^2 - {h_2}^2} \right)\,..................\left( 3 \right)$
From mathematics $\left( {{a^2} - {b^2}} \right) = \left( {a + b} \right)\left( {a - b} \right)$, by using this formula in RHS, then
$H\left( {{h_1} - {h_2}} \right) = \left( {{h_1} + {h_2}} \right)\left( {{h_1} - {h_2}} \right)$
By keeping $H$ in one side and the other terms in other side, then
$H = \dfrac{{\left( {{h_1} + {h_2}} \right)\left( {{h_1} - {h_2}} \right)}}{{\left( {{h_1} - {h_2}} \right)}}$
By cancelling the same terms in the above equation, then
$H = \left( {{h_1} + {h_2}} \right)$ or $H = \left( {{h_2} + {h_1}} \right)$
Thus, the above equation shows the height of water inside the tank.
Hence, the option (B) is correct.

Note:- In this problem, we have to give more concentration on cancelling the square root, both sides are having square roots so we cancel the square roots. And in equation (3), one mathematical formula is used, so the concentration is given in that step also. And in the final step both $\left( {{h_1} + {h_2}} \right)$ and $\left( {{h_2} + {h_1}} \right)$ are same.