Solveeit Logo
Login

Question

Question: A water jet from a fountain reaches its maximum height of \(4m\) at a distance \(0.5m\) from the ver...

A water jet from a fountain reaches its maximum height of 4m4m at a distance 0.5m0.5m from the vertical passing through the point O of the water outlet. The height of the jet above the horizontal OX at a distance of 0.75m0.75m from the point O is
(a).5m(a). 5m
(b).6m(b). 6m
(c).3m(c). 3m
(d).7m(d). 7m

Explanation

Solution

We need to figure out what is given. Here we get the parabola and we can also have the value of height and distance once we mark the point in a diagram we can easily get the height of the jet when the distance is 0.75m0.75m by using roots of the parabola.

Complete step by step solution:
A water jet from a fountain reaches its maximum height of 4m4m at a distance 0.5m0.5m from the vertical passing through the point O of the water outlet. So the jet starts at the initial point 00 which means (0,0)(0,0) and reaches the maximum height of 4m4m a distance 0.5m0.5m which means (0.5,4)(0.5,4) and the end point (0,1)(0,1) We need to find the height at a distance of 0.75m0.75m which means (0.75,h)(0.75,h).

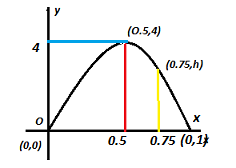
This represents the parabola, now we need to find the height of the jet above the horizontal OX at a distance of 0.75m0.75m from the point O
This is the parabola so the roots of the parabola are
⇒y=a(x−r)(x−s)\Rightarrow y=a(x-r)(x-s)
We take the point (0,1)(0,1) as r=0,s=1r=0,s=1
Apply this to the roots of the parabola,
⇒y=a(x−0)(x−1)\Rightarrow y=a(x-0)(x-1)
⇒y=ax(x−1)→(1)\Rightarrow y=ax(x-1)\to (1)
Now we take the maximum height of 4m4mat a distance of 0.5m0.5m so the xx coordinate is 0.5m0.5m and yycoordinate is 4m4m. Apply this to equation (1)(1)
⇒4=a(0.5)(0.5−1)\Rightarrow 4=a(0.5)(0.5-1)
Multiply this we get,
⇒4=a(0.5)(−0.5)\Rightarrow 4=a(0.5)(-0.5)
⇒a=−4(0.5)(0.5)\Rightarrow a=-\dfrac{4}{(0.5)(0.5)}
Multiply and divide by 100100 to take the decimal out
⇒a=−40025\Rightarrow a=-\dfrac{400}{25}
⇒a=−16\Rightarrow a=-16
Now apply this to equation (1)(1)we get,
⇒y=−16(x)(x−1)→(2)\Rightarrow y=-16(x)(x-1)\to (2)
Now using this we can the height of the jet above the horizontal OX at a distance of 0.75m0.75m, thus the xx coordinate is 0.75m0.75m and yycoordinate is hh
Apply this to equation (2)(2)
⇒h=−16(0.75)(0.75−1)\Rightarrow h=-16(0.75)(0.75-1)
⇒h=−16(0.75)(−0.25)\Rightarrow h=-16(0.75)(-0.25)
Multiply this we get,
⇒h=3m\Rightarrow h=3m

The height of the jet above the horizontal OX at a distance of 0.75m0.75m from the point O is 3m3m.

Note:
One more example for parabola, when liquid is rotated the forces of gravity result in the liquid forming a parabola-like shape. Definition of parabola is, it’s a locus of such a point which has an equal distance from a fixed line and a fixed point. The value of eccentricity for parabola is one.