Question

A water is being poured at the rate of 36 into a cylindrical vessel whose circular base is of radius 3m then the water level in cylindrial is rising at the rate of

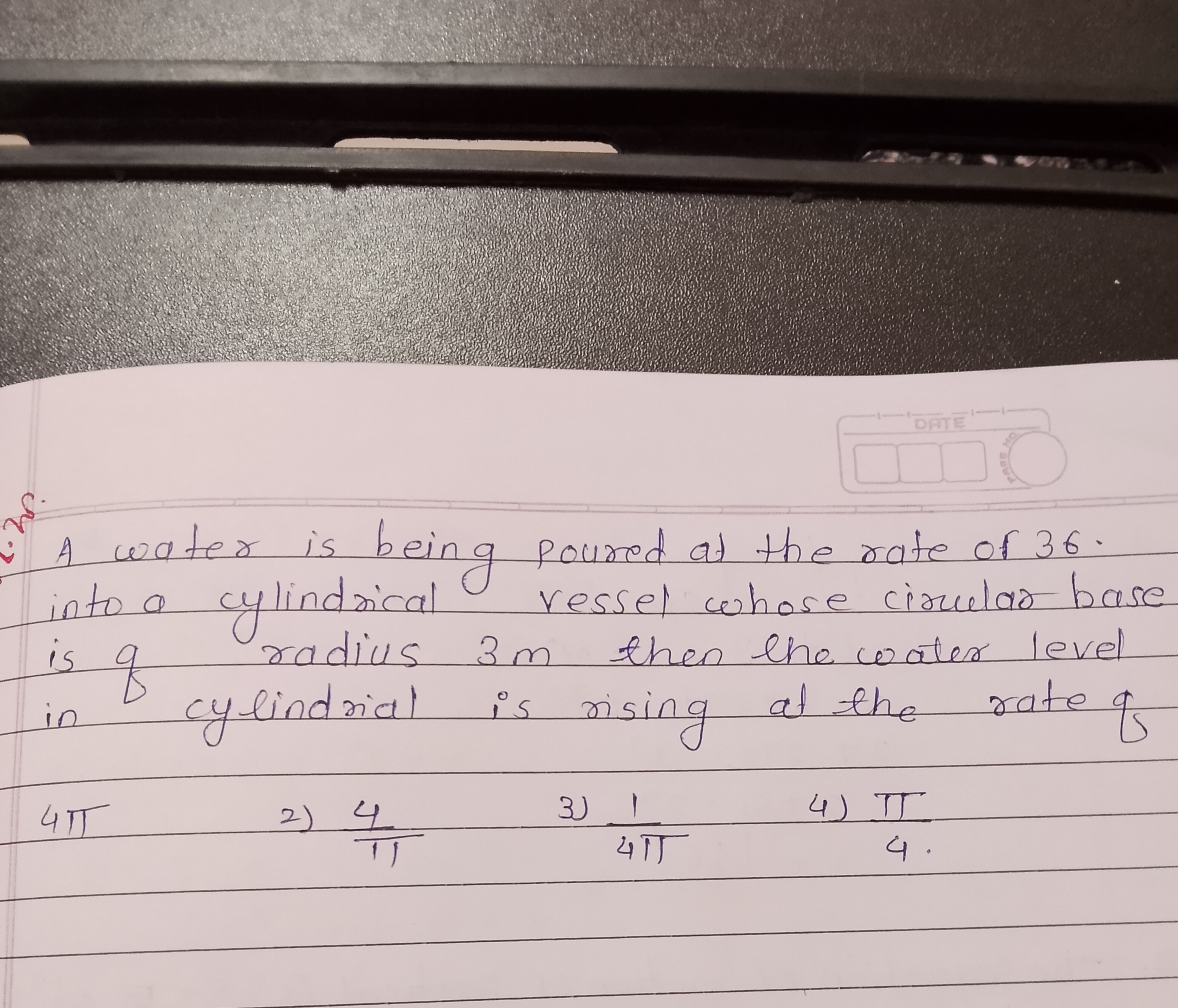
• A. $4\pi$
• B. $\frac{4}{\pi}$
• C. $\frac{1}{4\pi}$
• D. $\frac{\pi}{4}$

Answer 1

Answer: (B)

$\frac{4}{\pi}$

Answer 2

The volume of water in a cylindrical vessel is given by

$$V=\pi r^2 h.$$

For a cylinder with radius $r=3$ m,

$$V=9\pi h.$$

Differentiating both sides with respect to time $t$, we get

$$\frac{dV}{dt} = 9\pi \frac{dh}{dt}.$$

Given $\frac{dV}{dt} = 36$, solving for $\frac{dh}{dt}$ gives

$$\frac{dh}{dt} = \frac{36}{9\pi} = \frac{4}{\pi}.$$