Question

A water-filled cylinder of height 50 cm and base area $20 cm^2$ is placed on a table with the base on the table. The force offered by water on the table is:
(A) $98$
(B) $49$
(C) $9.8$
(D) $4.9$

Answer 1

This given problem can be solved by taking into the consideration of pressure exerted by the liquid on the surface of contact of the vessel. And we know the relationship between force and pressure, so the force can be calculated in that way.

Complete step by step answer:
Step 1: As it is given in the problem that a cylinder of height 50cm is filled with water and its cross-section area is $20 cm^2$. This cylinder is placed on a table with the base on the table.

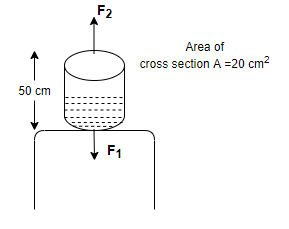
As shown in the above figure that if a force of amount $\mathop F\nolimits_1$ is applied by the liquid in the cylinder on the table and we know by Newton’s third law that there is always a reaction to an action that is equal in amount and opposite in the direction. So, the table will exert a force of equal amount on the cylinder but in the opposite direction and i.e., $\mathop F\nolimits_2$.
So, $\mathop F\nolimits_1 = \mathop F\nolimits_2$.
But the force acting vertically downwards on the table is equal to the weight, i.e.,
$\mathop F\nolimits_1 = Mg$ ………………………….. (1)
Step 2: In equation (1), mass can be calculated by taking the consideration of the volume of the liquid, i.e., $V$ and density of the liquid, i.e., $\rho$.
We know that density can be defined as
$\text{Density} = \dfrac{\text{Mass}}{\text{Volume}}$
So, $\rho = \dfrac{M}{V}$
Mass can be calculated from the above equation by rearranging it, i.e.,
$M = \rho V$ ………………………………... (2)
Where, $\rho =$density of water and $V =$volume of water
And, $\rho = 1.00 \times \mathop {10}\nolimits^3 kg/m^3$
Volume can be calculated by –
$\text{Volume= cross section area} \times \text{height}$
$\Rightarrow V = 20 \times \mathop {10}\nolimits^{ - 4} \times 50 \times \mathop {10}\nolimits^{ - 2}$
On further solving the above equation $V = \mathop {10}\nolimits^{ - 3}$
Step 2: By keeping all the values in the equation (2), we will get –
$\Rightarrow M = \rho V = \mathop {10}\nolimits^{ - 3} \times \mathop {10}\nolimits^3 = 1kg$
And $g = 9.8m/s^2$
So, keeping all the values in equation (1), we will get –
$\Rightarrow \mathop F\nolimits_1 = 1 \times 9.8 = 9.8N$.
So, the force exerted by the water on the table is $\mathop F\nolimits_1 = 9.8N$.

Hence, option (C) is correct.

Note:
The pressure exerted by the liquid column of height h is independent of the area of cross-section A but depends upon the height of the liquid column and density of the liquid $\rho$. But force depends upon both.