Question

A walnut can be broken by applying a direct force of 50kgf. If the walnut is placed in a nutcracker, the length of whose handle is 18 cm and nut is placed 2cm from the pivot, calculate the minimum force required to crack the nut.

Answer 1

We are given the minimum force to open a walnut and are asked to find the minimum force to crack the same nut using a nutcracker. We know that when we use a nutcracker, the net torque about the pivot of the nutcracker will be the same. Using this concept we will get the solution.

Formula used:
$\tau =F\times r$

Complete step by step answer:
In the question we are given the force required to break a walnut directly. It is said that the same walnut is placed in a nutcracker at a distance 2 cm from the pivot and the distance of the handle of the cracker is 18 cm.
Consider the figure given below.

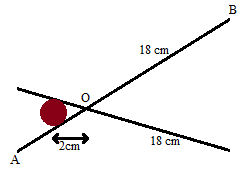
Here ‘O’ is the pivot. The distance from A to O is 2 cm and from B to O is 18 cm.
The minimum force required to break the nut directly is given as,
${{F}_{\min }}=50kgf$
This should be the force applied at A to break the nut.
Therefore the torque about the hinge due to the force at A will be,
$\tau =50\times 2$
$\Rightarrow \tau =100Ncm$
We will apply a force at the ends of the handle to apply the minimum force at A. let this force applied at the ends of the handle be ‘F’.
Therefore the torque felt at the hinge due to the force applied at B will be,
$\tau =F\times 18$
$\Rightarrow \tau =18F$
Now, we know that for the walnut to crack open, the net torque at the hinge should be zero. Therefore we can write,
$\Rightarrow 100=18F$
From this we will get the force applied at the handle as,
$\Rightarrow F=\dfrac{100}{18}$
$\therefore F=5.55N$
Hence, the minimum force required to break a walnut in a nutcracker is 5.55 N.

Note:
Here we know that the torque is constant in the system. So as the distance increases the force will decrease, i.e. to get a minimum resultant force we should apply the force at a maximum distance this is why we apply the force at the ends of the handle.