Question

A wall is moving with velocity $u$ and a source of sound moves with velocity $u/2$ in the same direction as shown in the figure. Assuming that the sound travels with velocity $10u$, the ratio of incident sound wavelength on the wall to the reflected sound wavelength by the wall is equal to

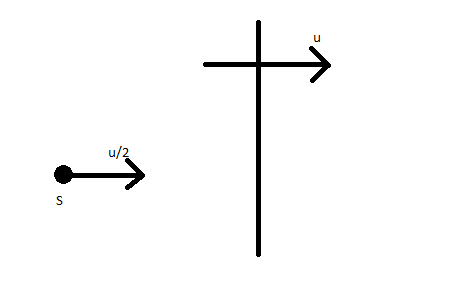
(A) $9:11$
(B) $11:9$
(C) $4:5$
(D) $5:4$

Answer 1

Hint We know that for constant velocity, the frequency of a wave is inversely proportional to the wavelength of the same wave. We will use this principle and do the problem with the equation of doppler effect for frequency change $\dfrac{{{f_{final}}}}{{{f_{initial}}}} = \dfrac{{{v_{sound}} - {v_{observer}}}}{{{v_{sound}} - {v_{source}}}}$.
Formula used:
$wavelength = \dfrac{{Speed\ Of\ Sound - Speed\ Source}}{{frequency}}$,
&, $\dfrac{{{f_{final}}}}{{{f_{initial}}}} = \dfrac{{{v_{sound}} - {v_{observer}}}}{{{v_{sound}} - {v_{source}}}}$.

Complete step by step answer
From the equations of the doppler effect, we get the final frequency equation as, $\dfrac{{{f_{final}}}}{{{f_{initial}}}} = \dfrac{{{v_{sound}} - {v_{observer}}}}{{{v_{sound}} - {v_{source}}}}$.

We will use this main equation to solve for this frequency change, where the source velocity is given as $u/2$ and the velocity of the reflecting wall is given to be $u$.
Let us assume that the frequency of sound received by the wall is $f\prime$ and $f$ is the initial source frequency of the sound. Thus, the ratio of frequencies from the above equation will be, $\dfrac{{f'}}{f} = \dfrac{{10u - u}}{{10u - \dfrac{u}{2}}} = \dfrac{{18}}{{19}}$.
$\Rightarrow f' = \dfrac{{18}}{{19}}f$.
We know
$wavelength = \dfrac{{Speed\ Of\ Sound - Speed\ Source}}{{frequency}}$.
Therefore the incident wavelength is
${\lambda _i} = \dfrac{{10u - u/2}}{f} = \dfrac{{9.5u}}{f}$
Now we will consider the frequency of the reflected sound from the wall to be $f\prime \prime$. Then using the same frequency equation as above, we get,
$\dfrac{{f''}}{{f'}} = \dfrac{{10u}}{{10u - ( - u)}}$,
here the source velocity is negative since it is directed opposite the direction of the sound.
$f'' = \dfrac{{10u}}{{10u + u}}f' = (\dfrac{{10}}{{11}})\dfrac{{18}}{{19}}f$.
This is the frequency of the reflected sound at the final observer.
Now the reflected wavelength is given by
${\lambda _f} = \dfrac{{10u + u}}{{f'}} = \dfrac{{11u}}{{f'}} = \dfrac{{11u}}{{18f}} \times 19$
We know wavelength and frequency are inversely proportional. Therefore, the required wavelength ratio of the incident sound wave to the reflected sound wave will be the same as the ratio of frequencies between the reflected sound wave and the incident sound wave. Here the ratio of the wavelengths is,
$\dfrac{{{\lambda _i}}}{{{\lambda _f}}} = \dfrac{{9.5u}}{f} \times \dfrac{{18f}}{{11u \times 19}}$
Therefore, the required ratio is
$\dfrac{{{\lambda _i}}}{{{\lambda _f}}} = \dfrac{9}{{11}}$.

The correct answer is option (A).

Note The direction of the sound is considered to be the positive direction for applying the formula of doppler frequency shift, i.e. $\dfrac{{{f_{final}}}}{{{f_{initial}}}} = \dfrac{{{v_{sound}} - {v_{observer}}}}{{{v_{sound}} - {v_{source}}}}$. Here when the direction of the sound changes, i.e. the direction of sound travelling is opposite to the speed of the actual movement of the observer or the source, then we will have to use a negative sign for the velocity of the observer or the source respectively.