Question

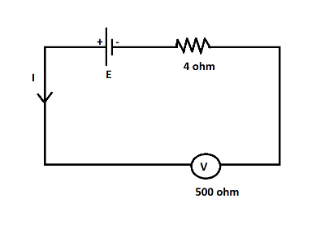
A voltmeter with resistance $500\Omega$ is used to measure the emf of a cell of internal resistance $4\Omega$ the percentage error in the reading of the voltmeter will be
A. 0.2%
B. 0.8%
C. 1.4%
D. 2.2%

Answer 1

To solve this question, we have to remember that, I drawn from the cell having emf E and external resistance R and internal resistance r can be given as: $I = \dfrac{E}{{R + r}}$

Complete answer:
Given that,
Resistance of the voltmeter, R = $500\Omega$
Internal resistance of the cell, r = $4\Omega$
We know that a voltmeter is used to measure the potential difference in a circuit.
So, the actual value for which the voltmeter is connected to measure = E.
Now we have to find the measure value of potential difference by the voltmeter.
We know that,
$I = \dfrac{E}{{R + r}}$
Putting the given values, we will get
$\Rightarrow I = \dfrac{E}{{500 + 4}}A \\\ \Rightarrow I = \dfrac{E}{{504}}A \\\$
Now,
Potential difference, V = IR
$\Rightarrow V = \dfrac{E}{{504}} \times 500 \\\ \Rightarrow V = \dfrac{{500E}}{{504}} \\\$
So, we can say the measure value of the potential difference by the voltmeter is $\dfrac{{500E}}{{504}}$ Volts.

We know that,
Error = actual value – measured value
Therefore,
Error = $E - \dfrac{{500E}}{{504}}$
Error = $\dfrac{{504E - 500E}}{{504}}$
Error = $\dfrac{{4E}}{{504}}$
Now, we have to find out the % error
Hence,
% error = $\dfrac{{{\text{error}}}}{{{\text{actual value}}}} \times 100$
Putting all the values, we will get
% error = $\dfrac{{\dfrac{{4E}}{{504}}}}{E} \times 100$
% error = $\dfrac{{400}}{{504}}$
% error = 0.8%
Hence, we can say that the percentage error in the reading of the voltmeter is 0.8%

So, the correct answer is “Option B”.

Note:
Whenever one asks such types of questions, first we have to identify the combination of the resistance, either they would be in series combination or parallel combination. In parallel combination, the potential difference across all of them is the same and current through any resistor is inversely proportional to its resistance.