Question

A voltmeter has a resistance G and range V. Calculate the resistance to be used in series with it to extend its range to $nV$.
A. $\left( {n - 2} \right)G$
B. $\left( {n - 1} \right)G$
C. $\left( {n - 4} \right)G$
D. $\left( {n - 2} \right)2G$

Answer 1

Express the current in the voltmeter before connecting the external resistance in the series. After connecting the external resistance in the series with voltmeter, the range of the voltmeter will increase to $nV$, where V is the voltage range of the voltmeter in the first case.

Formula used:
Ohm’s law, $V = IR$,
where, V is the voltage, I is the current and R is the resistance.

Complete step by step answer:
We know that when we connect an external resistance in series with the galvanometer, we can extend the range of the voltmeter.When the external resistance was not connected in series with the voltmeter, the voltage across the voltmeter is,
$V = {I_g}G$
$\Rightarrow {I_g} = \dfrac{V}{G}$ …… (1)
Here, ${I_g}$ is the current in the voltmeter and G is the resistance of the voltmeter.

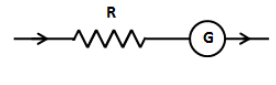
When we connect the external resistance in series with the voltmeter as shown in the above figure, the voltage across the voltmeter and resistance becomes,
$V' = {I_g}\left( {G + R} \right)$
We have given that when we connect the external resistance in series the range of the voltmeter is increased to $V' = nV$. Thus, the above equation becomes,
$nV = {I_g}\left( {G + R} \right)$
Using equation (1) in the above equation, we get,
$nV = \dfrac{V}{G}\left( {G + R} \right)$
$\Rightarrow n = \dfrac{{G + R}}{G}$
$\Rightarrow G + R = nG$
$\Rightarrow R = nG - G$
$\therefore R = \left( {n - 1} \right)G$
Thus, to increase the range of the voltmeter to $nV$, the value of external resistance should be $\left( {n - 1} \right)G$.

So, the correct answer is option B.

Note: We have used the fact that the current in the series connection remains the same. Therefore, the current in the external resistance and voltmeter is the same. If we connect the external resistance across the voltmeter, the range of the voltmeter decreases since the current also flows through the external resistance.