Question

A vessel with water is placed on a weighing pan and it reads $600$gm. Now, a ball of mass $40$gm and density $0.80g/c{{m}^{-3}}$is sunk into the water with a pin of negligible volume, as shown in figure. The weighing pan will show a reading:

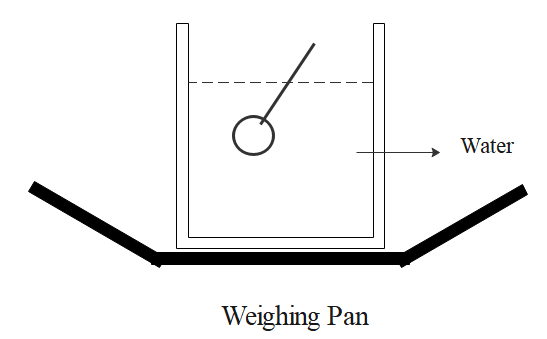
a)$600gm$
b)$550gm$
c)$650gm$
d)$632gm$

Answer 1

Calculate the volume of the ball given and then find out the weight of it. Then, add it up with the existing weight. Also, the mass of the pin is negligible, neglecting the weight of it in the total measurement. Weight and mass are not the same.
Formula used:
$d=\dfrac{m}{v}$

Complete answer:
Let us assume the density of the given ball is $d$, the mass of the ball as $m$and the volume of the ball as $v$. Now, the volume of the ball must be calculated,
$\begin{aligned} & d=\dfrac{m}{v} \\\ & v=\dfrac{m}{d} \\\ & v=\dfrac{40}{0.80} \\\ & v=50c{{m}^{3}} \\\ \end{aligned}$
Now, the total weight must be calculated in the following way,
total weight =
$\begin{aligned} & 600+50 \\\ & 650 \\\ \end{aligned}$

Therefore, the weighing pan will display as $650$, option c.

Additional information:
The weight of an object is the force of gravity on the object and maybe defined as the mass times the acceleration of gravity. As weight is a force, the SI unit of the weight is Newton. The density of a substance is its mass per unit volume. For a pure substance, the density has the same numerical value as its mass concentration. The density can be related to buoyancy, purity and packaging.

Note:
As mass is given in the question, the weighing machine doesn’t display the value of given mass and existing value. There’s a difference between mass and weight. Weight is the mass times the gravity. So, instead, we can find the volume of the ball and add it to the existing value.