Question

A vessel of depth $x$ is half filled with a refractive index ${{\mu }_{2}}$. The apparent depth as viewed from above is:
a)$\dfrac{x({{\mu }_{1}}+{{\mu }_{2}})}{2{{\mu }_{1}}{{\mu }_{2}}}$
b)$\dfrac{x{{\mu }_{1}}{{\mu }_{2}}}{2({{\mu }_{1}}+{{\mu }_{2}})}$
c)$\dfrac{x{{\mu }_{1}}{{\mu }_{2}}}{({{\mu }_{1}}+{{\mu }_{2}})}$
d)$\dfrac{2x({{\mu }_{1}}+{{\mu }_{2}})}{{{\mu }_{1}}{{\mu }_{2}}}$

Answer 1

Apparent depth is the depth of the object in a denser medium as viewed from a rarer medium. It is usually smaller than the real depth. The apparent depth is the actual depth divided by the refractive index.

Formula used:
${{D}_{apparent}}=\dfrac{{{D}_{real}}}{\mu }$

Complete answer:
Real depth is the actual distance of an object beneath the surface, as would be measured by submerging a perfect ruler along with it. Apparent depth is the depth of an object in a denser medium as seen from the rarer medium. The value is smaller than the actual depth.

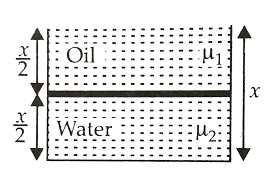
Let, the refractive index of oil be ${{\mu }_{2}}$, depth of vessel be $x$.The refractive index of air medium be ${{\mu }_{1}}$.
The apparent depth will then be,
$\begin{aligned} & {{D}_{apparent}}=\dfrac{x}{2{{\mu }_{1}}}+\dfrac{x}{2{{\mu }_{2}}} \\\ & {{D}_{apparent}}=\dfrac{x}{2}\left( \dfrac{{{\mu }_{1}}+{{\mu }_{2}}}{{{\mu }_{1}}{{\mu }_{2}}} \right) \\\ \end{aligned}$

So, the correct answer is “Option B”.

Additional Information:
When an object placed in a denser medium is viewed from a rarer medium, the object appeared to be at a lesser depth. The diameter of the pupil of the human eye is in the range of seven millimeters. So, when we are looking down into the pool, the angles involved are small. That is why, when we look down into the pool of water from above, the pool from above, looks less deeply than it really is. The velocity and direction of the ray changes due to refraction which results in false appearance of depth of material.

Note:
This phenomenon occurs due to the property of light called refraction of light. When a stick is immersed in water or any other medium, the part of the stick which is in water only undergoes change in shape and size, whereas, the part that is outside the medium will be the same.