Question
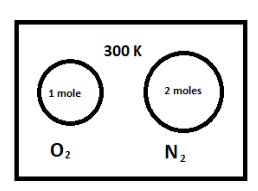
Question: A vessel contains a mixture of one mole of oxygen and two moles of nitrogen at 300 K. The ratio of t...
A vessel contains a mixture of one mole of oxygen and two moles of nitrogen at 300 K. The ratio of the average rotational kinetic energy per O2 molecules to that per N2 molecules is
A. 1:1
B. 1:2
C. 2:1
D. Depends on the moment of inertia of the two molecules
Solution
To find the ratio of the average rotational kinetic energy per molecule of the oxygen and nitrogen present in the mixture, we will use the law of equipartition of energy stating the equal distribution of energy among the degrees of freedom of the respective molecules. The degrees of freedom can be calculated using the formula:
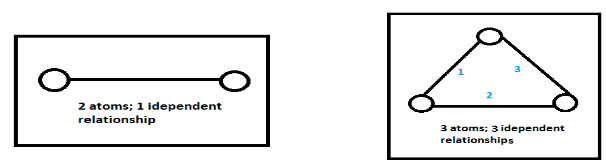
Df=3N−K where N is the number of particles and K is the independent relations among these particles.
Complete step by step answer:
It is given that we have one mole of oxygen (O2) gas and two moles of nitrogen (N2) gas at the temperature 300K.
Now, according to the law of equipartition of energy:
When a system is in equilibrium (thermal), the total energy of the system is divided equally among all the degrees of freedom. Thus, the average rotational kinetic energy will also be divided equally among all the degrees of freedom for the moles of both the gases.
This average energy is given as:
E=21KT....(1) where K is the Boltzmann’s constant and T is the temperature.
The temperature is constant for this system, the system will be in thermal equilibrium and this energy will be dependent on the degrees of freedom of respective gases. The degrees of freedom can be calculated using the formula Df=3N−K where N is the number of particles and K is the independent relations among these particles.
For O2 molecules, the degree of freedom can be calculated as:
Df=3N−K here,
Number of molecules (N) = 2
Independent relations among them (K) = 1 (known)
{D_{{f_{{O_2}}}}} = 3 \times 2 - 1 \\\
\Rightarrow {D_{{f_{{O_2}}}}} = 6 - 1 \\\
\Rightarrow {D_{{f_{{O_2}}}}} = 5 \\\
For N2 molecules, the degree of freedom can be calculated as:
Df=3N−K here,
Number of molecules (N) = 2
Independent relations among them (K) = 1 (known)
{D_{{f_{{N_2}}}}} = 3 \times 2 - 1 \\\
\Rightarrow {D_{{f_{{N_2}}}}} = 6 - 1 \\\
\Rightarrow {D_{{f_{{N_2}}}}} = 5 \\\
The ratio of average energy of the molecules will be equal to the ratio of their degrees of freedom as the energy is divided equally amongst them. So the required ratio for both the gases is given as:
EN2EO2=DfN2DfO2
Substituting the values, we get:
\dfrac{{{E_{{O_2}}}}}{{{E_{{N_2}}}}} = \dfrac{1}{1} \\\
\therefore {E_{{O_2}}}:{E_{{N_2}}} = 1:1 \\\
Therefore, the ratio of the average rotational kinetic energy per O2 molecules to that per N2 molecules is 1: 1 and the correct option is A.
Note: The independent relations K among the molecules is generally known for monoatomic (having one atom), diatomic (having 2 atoms) and triatomic gases (having 3 atoms) as 0, 1 and 3 respectively. But, we can also find by drawing the number of molecules and finding the independent relations if forgotten as: 1 atom cannot have an independent relationship with any other atom, so it’s count is 0.