Question
Question: A vessel ABCD of 10 cm width has two small slits \({{S}_{1}}\) and \({{S}_{2}}\) sealed with identic...
A vessel ABCD of 10 cm width has two small slits S1 and S2 sealed with identical glass plates of equal thickness. The distance between slits is 0.8 mm. PQ is the line perpendicular to the plane AB and passing through O, the middle point of S1 and S2. A monochromatic light source is kept at S, 40 cm below P and 2 m from the vessel, to illuminate the slits as shown in the figure below. Calculate the position of the central bright fringe on the other wall CD with respect to the line OQ. Now, a liquid is poured into the vessel and filled up to OQ. The central bright fringe is found to be at Q. Calculate the refractive index of the liquid.
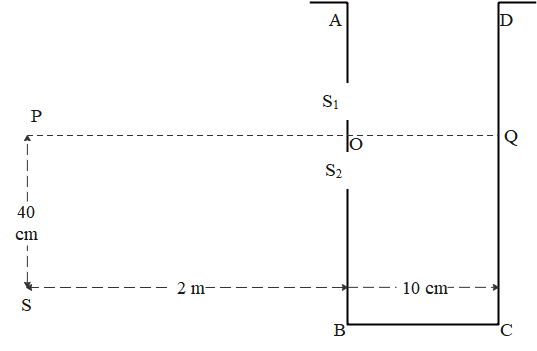
Solution
This question is related to Young’s double slit experiment. Central maxima is obtained, when the path difference between two coherent waves is zero. Use this concept, to derive a relation for distance of central bright fringe from Q. When liquid is introduced, path length passing from liquid increases by a multiple of refractive index. Use this fact, to obtain an expression for the position of the central bright fringe after liquid is introduced. Then solve the equation for refractive index.
Formula used: For central fringe in double slit experiment, path difference Δz=0
Complete step by step answer:
We assume that central fringe is formed at distance x2 from Q. Let us assume this position to be R. Since path difference for central fringe is zero, therefore
(SS1+S1R)−(SS2+S2R)=0
(SS1−SS2)=(S2R−S1R)
Using Pythagoras theorem, in triangle SBS1, SBS2,S1RQandS2RQ we get
(SS1)2=D12+(x1+2d)2⇒SS12=D121+D1x1+2d2
(SS2)2=D12+(x1−2d)2⇒(SS2)2=D121+D1x1−2d2
(S1R)2=D22+(x2−2d)2
(S2R)2=D22+(x2−2d)2
We have assumed S1RQandS2RQ as right-angled triangle as S1Q=S2Q=2d is very small and can be neglected.
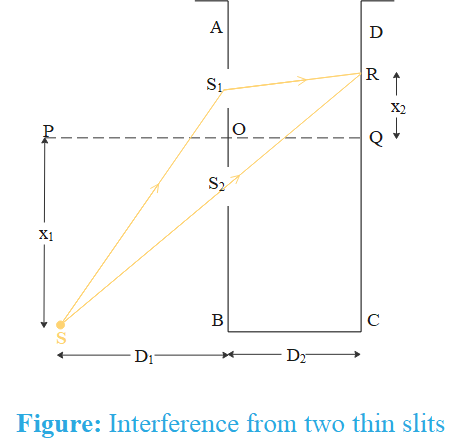
Now, we assume that D1≫x1,d and D2≫x2,d, then
SS1=D11+D12x12+x1d+4d221≈D1+2D1x12+2D1x1d+8D1d2
Similarly,
SS2=D11+D12x12−x1d+4d221≈D1+2D1x12−2D1x1d+8D1d2
⇒SS1−SS2=D1x1d
In a similar way, we obtain
S2R−S1R=D2x2d
∵(SS1−SS2)=(S2R−S1R)
∴D1x1d=D2x2d⇒x2=D1D2x1
Substituting the values of D1=2m=200cm;D2=10cm;and x1=40cm, we have
x2=20010×40=2cm
When liquid is poured into the vessel and filled up to OQ, the central fringe shifts to Q. For the central fringe to be at Q, Path difference must be zero.
(SS1+S1Q)−(SS2+μS2Q)=0
⇒SS1−SS2=μS2Q−S1Q
⇒D1x1d≈μ(D22+4d2)1/2−(D22+4d2)1/2=(μ−1)(D22+4d2)1/2
D1x1d=(μ−1)D2(1+4D22d2)≈(μ−1)D2
Substituting the values, we get
200cm40cm×0.08cm=(μ−1)×10cm
⇒μ=1.0016
The refractive index of liquid is 1.0016.
Note: The path length of the wave changes to μ index times its path length in free space when it passes through a material of refractive index μ.
In this question, values of different lengths are given in different units. When using these values in formula, they must be changed to the same unit first.
