Question

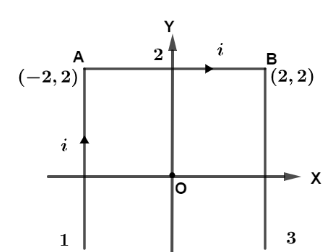
A very long wire is bent as shown in the figure. The segment $1$ and $3$ are infinitely long and parallel to Y axes. The segment $2$ is a finite wire parallel to X axes. The wire carries current $i$ . The magnetic field at the origin is:

A. $\dfrac{{{\mu _0}i}}{{4\pi }}(1 + \sqrt 2 )(\hat k)$
B. $\dfrac{{{\mu _0}i}}{{4\pi }}(1 + \sqrt 2 )( - \hat k)$
C. Zero
D. None of these

Answer 1

In order to find a net magnetic field at the origin O, we will use the general formula of magnetic field due to infinite wire and magnetic field due to finite wire, and add them using vector algebra. Magnetic field direction due to clockwise flowing current in a wire in XY plane will be in downward direction which is in $- \hat k$

Formula used:
Magnetic field due to a wire is
$B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{i}{a}(\sin {\phi _1} + \sin {\phi _2})$
where, ${\phi _1}(and){\phi _2}$ are the angles made by two ends of the wire to the line joining between the midpoint of the wire and to the point where the magnetic field is measured. $a$ Is the perpendicular distance between wire and the line joining to the point where the magnetic field is to be measured.

Complete step by step answer:
Let us first draw the diagram, from the geometry of figure we can see that, the angles made by segment $1$ and $3$ which are infinite wires are ${45^0}(and){90^0}$ and from geometry we see that $OP = OQ = 2units.$.

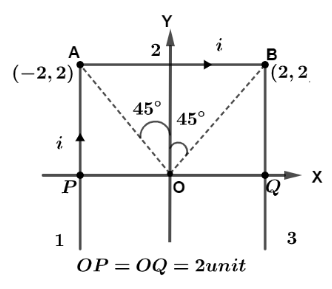
So, for segment $1$ and $3$ we have equal magnetic fields which can be calculated by putting the values in formula $B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{i}{a}(\sin {\phi _1} + \sin {\phi _2})$
${\phi _1}(and){\phi _2}$ is equals to ${45^0}(and){90^0}$
$a = 2\,units$ So,
${B_1} = {B_3} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{i}{2}(\sin {45^0} + \sin {90^0})$
$\Rightarrow {B_1} = {B_3} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{i}{2}(1 + \dfrac{1}{{\sqrt 2 }})( - \hat k) \to (i)$

Now, for segment $2$ we can see from the diagram that, the angles for this segment is
${\phi _1}(and){\phi _2}$ Is equals to ${45^0}(and){45^0}$
$a = 2\,units$ So,
Again, putting these values in formula $B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{i}{a}(\sin {\phi _1} + \sin {\phi _2})$ we get,
${B_2} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{i}{2}(\sin {45^0} + \sin {45^0})$
$\Rightarrow {B_2} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{i}{2}(\sqrt 2 )( - \hat k) \to (ii)$
Now, if $B$ is the net magnetic field at origin O then,
$B = {B_1} + {B_3} + {B_2}$
On putting the values we get,
$B = 2 \times \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{i}{2}(1 + \dfrac{1}{{\sqrt 2 }})( - \hat k) + {B_2} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{i}{2}(\sqrt 2 )( - \hat k)$
$\therefore B = \dfrac{{{\mu _0}i}}{{4\pi }}(1 + \sqrt 2 )( - \hat k)$

Hence, the correct option is B.

Note: It should be remembered that, current is flowing in clockwise direction which produce magnetic field into the paper which is in negative Z direction and the value of basic trigonometric ratios are $\sin {45^0} = \dfrac{1}{{\sqrt 2 }}$ and $\sin {90^0} = 1$ ,${\mu _0}$ is known as the permeability of free space and the SI unit of magnetic field is Tesla.