Question

A very long straight wire of radius r carries current I. Intensity of magnetic field B at a point, lying at a perpendicular distance ‘a’ from the axis is $\propto$___________.
A. ${a}^{2}$
B. $\dfrac {1}{{a}^{2}}$
C. $\dfrac {1}{a}$
D. a

Answer 1

This problem can be solved using the Biot-Savart law which gives the expression for magnetic field in a long current carrying wire. Biot-Savart law helps us to calculate the magnetic field due to a steady current. From the expression for Biot-Savart law, we can infer that the magnetic field in a long current carrying wire is independent of the relative angular position of the point of observation. But it depends on the perpendicular distance from the wire.
Formula used:
$B=\dfrac { { \mu }_{ 0 }I }{ 2\pi r }$

Complete answer:

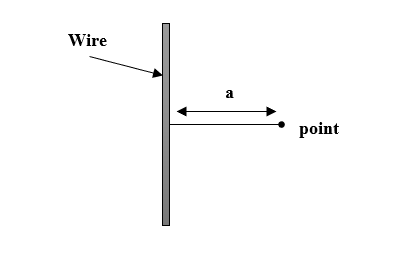
According to Biot-Savart’s law, magnetic field due to a very long straight wire is given by,
$B=\dfrac { { \mu }_{ 0 }I }{ 2\pi r }$ …(1)
Where, ${mu}_{0}$ is the constant
r is the distance from the wire
I is the current flowing through the wire
It is given that the perpendicular distance of the point from the wire is a.
Substituting this in the equation. (1) we get,
$B=\dfrac { { \mu }_{ 0 }I }{ 2\pi a }$
From above equation it can be inferred that,
$B \propto \dfrac {1}{a}$
Hence, intensity of a magnetic field at a perpendicular distance from a very long current carrying wire is proportional to $\dfrac {1}{a}$.

So, the correct answer is “Option C”.

Note:
Students may think that the electrons never stop moving, so it will always produce an electric field and hence the magnetic field. But in reality, this does not happen. Electrons move in a random direction in a conductor and thus, they get cancelled. Hence, the net electric field and magnetic field will be zero. When potential difference is applied across the terminals of the wire, electrons move in a specific direction. Hence, it will constitute current. As long as the potential difference exists, current through the wire exists and thus magnetic field exists for that same duration.