Question
Question: A very long rectangular box is divided into \( N \) equal compartments with \( \left( N-1 \right) \)...
A very long rectangular box is divided into N equal compartments with (N−1) fixed semipermeable in only first compartment and they can pass through only those SPM whose number is less than or membranes (SPM) numbered from 1 to (N−1) as shown in the figure. The gases are initially present equal to their subscript. For example, gas A1 can pass through only the first SPM; gas A2 can pass only through the first and second SPM, and so on. If initially all gases have the same moles and after a long time, the ratio of partial pressures of gas A4 in the third compartment to that of gas AN−1 in first compartment is 3, the value of N is?
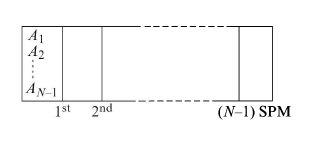
Solution
Hint : We know that the Dalton's Law of Partial Pressures states that the total Pressure exerted by the mixture of gases is equal to the sum of Partial Pressure of each individual Gas present. Each gas is assumed to be an ideal gas and given by formula PAN−1PA4=n/Nn/5=3
Complete step by step solution:
The mole fraction of a specific gas in a mixture of gases is equal to the ratio of the partial pressure of that gas to the total pressure exerted by the gaseous mixture. This mole fraction can also be used to calculate the total number of moles of a constituent gas when the total number of moles in the mixture is known
Since A1 can pass only through first 5Pm
i.e. A1 will be present in first & second compartment which is given by A2 will be in 1,2,3 and A3 in 1,2,3,4
and so on we earlier got the fraction value PAN−1PA4=n/Nn/5=3
By taking denominator in numerator we get;
PAN−1PA4=5n×nN=3
Thus we get
PAN−1PA4=5N=3 i.e. ⇒5N=3
| A1=2n | A1=2n | A2=3n |
|---|---|---|
| A2=3n | A2=3n | A3=4n |
| A3=4n | A3=4n | A3=4n |
Note :
Note that the applications of Dalton's partial pressures definition in the determination of pressure of a dry gas .In the calculation of partial pressure, expressing Partial Pressures in Terms of Mole Diffraction: the volume occupied by a specific gas in a mixture can also be calculated with this mole diffraction.
