Solveeit Logo
Login

Question

Question: A vertical wire carries a current in upward direction. If an electron beam sent horizontally towards...

A vertical wire carries a current in upward direction. If an electron beam sent horizontally towards the wire, then it will deflected
A. Vertically downwards and perpendicular to the plane of the paper
B. Vertically upwards and perpendicular to the plane of the paper
C. In the plane of the paper
D. No deflection

Explanation

Solution

Assume the electron is approaching from the left towards the wire. Using the right-hand thumb rule, determine the direction of the magnetic field. Specify the direction of velocity vector of electron and magnetic field on the axes and using the formula for magnetic force, determine the direction of the magnetic force.

Complete answer:
To answer this question, we first have to determine the direction of the magnetic field generated by the motion of the current flow. To find the direction of the magnetic field, we have to recall the right-hand thumb rule which states that if we hold the current carrying conductor in our right hand such that the direction of the thumb denotes the direction of the current flow; then the curled fingers around the conductor will denote the direction of the magnetic field.Thus, from the right-hand thumb rule, we can say that the direction of the magnetic field is into the page at the position of the electron.

Let’s consider the electron is sent from the left towards the wire. In the vicinity of the magnetic field, the magnetic force will act on the electron. We have the expression for the magnetic force acting on the charged particle,
F⃗=−e(v⃗×B⃗)\vec F = - e\left( {\vec v \times \vec B} \right)
Here, e is the charge of an electron, v is the velocity of the electron and B is the magnetic field.

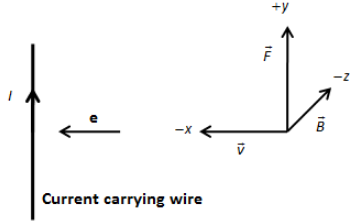
From the above figure, the magnetic field is along the −z−- z -axis and the velocity vector of the electron is along the−x−- x -axis. Therefore, we can determine the direction of force as,
F⃗=−e(v(−i^)×B(−j^))\vec F = - e\left( {v\left( { - \hat i} \right) \times B\left( { - \hat j} \right)} \right)
∴F⃗=evBk^\therefore \vec F = evB\hat k
Thus, the direction of magnetic force is along the positive direction of the y-axis that is vertically upward perpendicular to the plane of the paper.

So, the correct answer is option B.

Note: If instead of electron, the charge is proton, the magnetic force acting on the proton would be along the negative y-axis. Therefore, the deflection of the proton would be downwards. In this solution we have assumed that the electron is approaching from the left and if we consider the electron is approaching from the right, the result would be the same.