Question

A vertical wire carries a current in upward direction. An electron beam sent horizontally towards the wire will be deflected (gravity free space).
A. Towards right
B. Towards left
C. Upwards
D. Downwards

Answer 1

When a current passes through a conductor it produces a magnetic field. When an electron beam will be deflected, we first determine the direction of the magnetic field in the electron field then we determine the direction of force acting on the beam.

Formula Used:
The formula of the force exerted by the magnetic field is given by
$\vec F = q\left( {\vec v \times \vec B} \right)$
Here, $q$ is the charge on the conductor, $v$ is the velocity of charge and $B$ is the magnetic field.

Complete step by step answer:
Consider a vertical wire in which a current is moving in the upward direction. On this wire, an electron beam is sent horizontally.

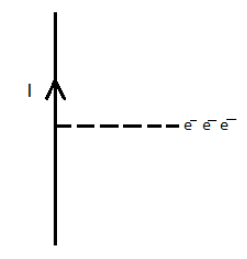
As the electron beam is moving toward the left or in the negative X-axis direction, therefore, the velocity of the electron $= v\left( { - \hat i} \right)$

Now, as the electron beam is sent horizontally, therefore, the direction of the magnetic field of the electron beam is in the upward direction or along the Y-axis. Therefore, the magnetic field of the electron beam $= \vec B\hat j$
Now, the force exerted by this magnetic field is given by
$\vec F = q\left( {\vec v \times \vec B} \right)$

Now, the charge on the electron is negative, therefore, the charge of the electron $= - q$
Therefore, the force due to the magnetic field on the electric field is given by
$\vec F = - q\left( {v( - \hat i) \times B(\hat j)} \right)$
$\therefore\vec F = - ( - \hat k) = \hat k$
Hence, the force acting on the electron beam is in a downward or Z-axis direction. So, this force will deflect the wire in the X-Y plane.

Hence, the wire will be deflected in an upward direction.Hence, option C is the correct option.

Note: An alternate way to solve the above question is given below. We can also use the Right-hand thumb rule to determine the direction of the magnetic field of the electron beam. After that we will use Fleming’s-left hand thumb rule to determine the force acting due to the magnetic field of the electron beam.