Question

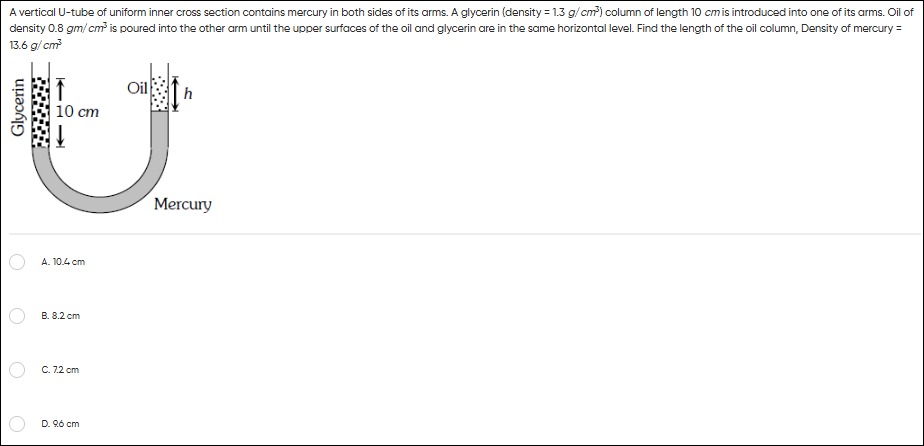
A vertical U-tube of uniform inner cross section contains mercury in both sides of its arms. A glycerin (density = 1.3 $g/cm^3$) column of length 10 cm is introduced into one of its arms. Oil of density 0.8 $gm/cm^3$ is poured into the other arm until the upper surfaces of the oil and glycerin are in the same horizontal level. Find the length of the oil column, Density of mercury = 13.6 $g/cm^3$

• A. 10.4 cm
• B. 8.2 cm
• C. 7.2 cm
• D. 9.6 cm

Answer 1

Answer: (D)

9.6 cm

Answer 2

The principle of fluid statics states that the pressure at the same horizontal level in a continuous fluid is equal. Let $h_g$ be the length of the glycerin column and $h_o$ be the length of the oil column. Let $\rho_g$, $\rho_o$, and $\rho_m$ be the densities of glycerin, oil, and mercury, respectively. Given: $h_g = 10$ cm, $\rho_g = 1.3$ g/cm$^3$, $\rho_o = 0.8$ g/cm$^3$, $\rho_m = 13.6$ g/cm$^3$.

Consider a horizontal level at the interface between glycerin and mercury in the left arm. The pressure at this level is $P_{left} = P_{atm} + \rho_g g h_g$. In the right arm, at the same horizontal level, the pressure is $P_{right} = P_{atm} + \rho_m g (h_{mR} - h_{mL}) + \rho_o g h_o$, where $h_{mR} - h_{mL}$ is the difference in mercury levels. Since the upper surfaces of oil and glycerin are at the same level, the difference in mercury levels is $h_{mR} - h_{mL} = h_g - h_o$. Equating pressures: $\rho_g h_g = \rho_m (h_g - h_o) + \rho_o h_o$. Rearranging for $h_o$: $h_o (\rho_m - \rho_o) = h_g (\rho_m - \rho_g)$. $h_o = h_g \frac{\rho_m - \rho_g}{\rho_m - \rho_o} = 10 \text{ cm} \times \frac{13.6 - 1.3}{13.6 - 0.8} = 10 \times \frac{12.3}{12.8} \approx 9.609$ cm.