Question

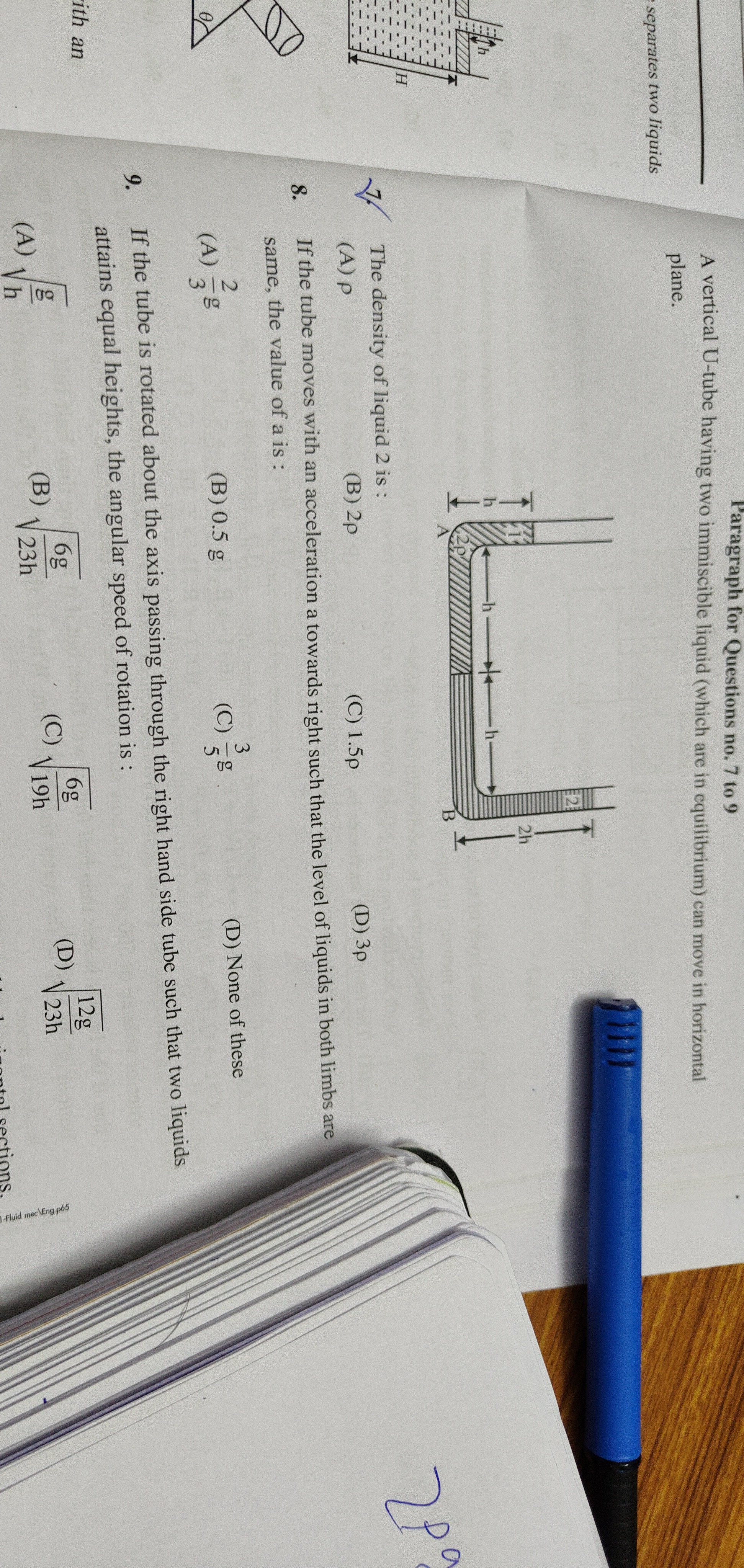
A vertical U-tube having two immiscible liquid (which are in equilibrium) can move in horizontal plane.

7. The density of liquid 2 is: (A) ρ (B) 2ρ (C) 1.5p (D) 3p

8. If the tube moves with an acceleration a towards right such that the level of liquids in both limbs are same, the value of a is : (A) $\frac{2}{3}g$ (B) 0.5 g (C) $\frac{3}{5}g$ (D) None of these

9. If the tube is rotated about the axis passing through the right hand side tube such that two liquids attains equal heights, the angular speed of rotation is : (A) $\sqrt{\frac{g}{h}}$ (B) $\sqrt{\frac{6g}{23h}}$ (C) $\sqrt{\frac{6g}{19h}}$ (D) $\sqrt{\frac{12g}{23h}}$

• A. ρ
• B. 2ρ
• C. 1.5p
• D. 3p

Answer 1

The provided solution does not contain the correct answer for question 7.

Answer 2

The provided solution for question 7 is incomplete and does not lead to a definitive answer from the given options. It repeatedly reaches the conclusion that $\rho = \rho_2$, which contradicts the options. A correct approach would involve considering the pressure at the interface. If we assume the diagram implies that the vertical height of liquid 1 is $h$ and the horizontal length is $h$, and for liquid 2, the vertical height is $h$ and the horizontal length is $2h$, then the pressure at the interface in the left limb is $P_{atm} + \rho g h$. In the right limb, the pressure at the interface would be $P_{atm} + \rho_2 g h$. For equilibrium, these must be equal, leading to $\rho = \rho_2$. However, if we interpret the diagram such that the total length of liquid 1 from the free surface to the interface is $h$ and the horizontal part is also filled with liquid 1 of length $h$, and for liquid 2, the vertical height is $h$ and the horizontal part is filled with liquid 2 of length $2h$, then the pressure at the interface in the left limb is $P_{atm} + \rho g (h+h) = P_{atm} + 2\rho g h$. In the right limb, the pressure at the interface is $P_{atm} + \rho_2 g (h+2h) = P_{atm} + 3\rho_2 g h$. Equating these gives $2\rho g h = 3\rho_2 g h$, so $\rho_2 = \frac{2}{3}\rho$. This also does not match the options. Without a clear interpretation of the diagram or additional information, question 7 cannot be definitively answered from the given options.