Question
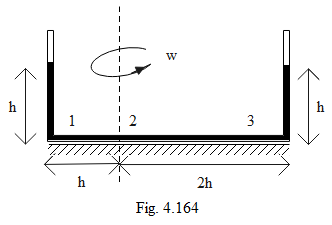
Question: A vertical U-tube has a liquid up to a height of h. If the tube is slowly rotated to an angular spee...
A vertical U-tube has a liquid up to a height of h. If the tube is slowly rotated to an angular speed ω=g/h, find the
(i) heights of the liquid column,
(ii) pressure at the points 1,2 and 3 in the limbs in steady state.
Explanation
Solution
As the tube is slowly rotated to an angular speed, so, we will consider a mass element at some distance from the axis of rotation. Then, we will consider the equation of the circular motion for this element in terms of the pressure, area, mass and angular frequency. After integrating this equation, we will get the required results.
Formula used:
P=AF
Complete answer:
Take a mass element at a distance x from the axis of rotation.
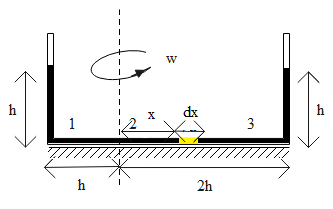
The equation of the circular motion for this element is,
