Question
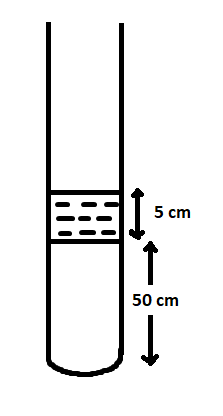
Question: A vertical tube of length \(100cm\) contains a mercury pallet of length \(5cm\) as shown in the figu...
A vertical tube of length 100cm contains a mercury pallet of length 5cm as shown in the figure. Air is trapped between the mercury pallet and the base of the tube. The length (cm) of the tube above the mercury pallet if the tube is inverted is nearly (1atm=75cmofHg) . Assume air to be ideal gas and temperature to be constant.
Solution
We have a tube and its length is given. There is a pallet of mercury at a given height and the air is trapped between the base of the tube and the mercury pallet. We have to find the length of the tube above the mercury pallet if the tube is inverted. The pressure of the atmosphere is given.
Complete step by step answer:
The air trapped between the base of the tube and the mercury pallet will experience pressure due to the mercury pallet and the pressure due to the atmosphere.
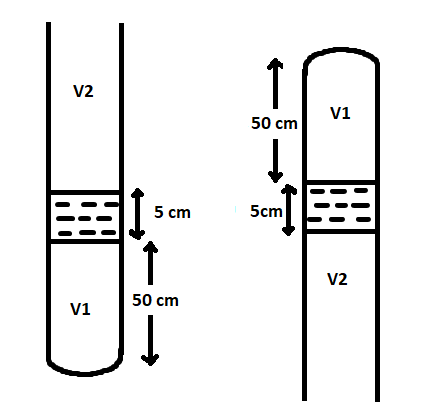
Let A be the cross-sectional area of the tube.
Let V1 be the volume of the tube below the mercury pallet.
V1=h×A
where h is the height of volume V1.
The height of mercury pallet is given as, 5cm=0.05m
Let PHg be the pressure exerted by the mercury and Patm be the pressure exerted by the atmosphere.
When the tube is vertically inverted, the pressure on the trapped air be,
Patm=PHg+Pair
According to Pascal’s law, the pressure P=hρg
Where Pstands for the pressure of the fluid, hstands for the height, ρ stands for the density of the fluid, and g stands for the acceleration due to gravity.
The height of the atmosphere above the mercury pallet is given as, 75cm=0.75m
The pressure of the atmosphere can be written as, Patm=0.75ρg
The height of mercury pallet is given as, 5cm=0.05m
Therefore, the pressure of mercury can be written as, PHg=0.05ρg
Therefore we can write the equation
Patm=PHg+Pair as,
⇒0.75ρg=Pair+0.05ρg
From this,
Pair=0.75ρg−0.05ρg=0.70ρg
When the tube is kept upright,
The pressure experienced by the trapped air can be written as, Pair=PHg+Patm
Now, we can write the total pressure on the trapped air as,
Pair=0.05ρg+0.75ρg=0.80ρg
According to Boyle’s law,
P1V1=P2V2
We know that Volume V=h×A
where his the height and A stands for the area.
Now we can substitute the values of pressure and volume in Boyle’s law to get
0.70ρg×h×A=0.80ρg×50×A
Cancelling common terms,
0.70h=0.80×50
From this, we get the height as,
h=0.700.80×50≈57.14cm
Hence, 57.14cm is the answer.
Note: When the fluid is at rest, at any point in the same horizontal level, the fluid will have the same pressure. The pressure will be the same in all directions at any point in a liquid that is at rest. The pressure is always acting normal to the area whatever maybe the orientation of the area.
