Question

A vertical row of trees 12m long casts a shadow 8m long on the ground, at the same time a tower casts the shadow 40m long on the ground. Determine the height of the tower.

Answer 1

In this problem we need to take two different triangles. In the first one we have to calculate the value of angle applicable. Then in the second triangle apply that angle with suitable trigonometry ratios. Thus we can find the height of the tower from the second triangle.

Complete step-by-step answer:
Let's draw two right angled triangles ABC and PQR. First triangle will be for the tree and the second triangle will be for the tower.
We have been given a vertical row of tree 12m long tree that casts a shadow 8m long on the ground. So, we make a $\vartriangle ABC$as follows,

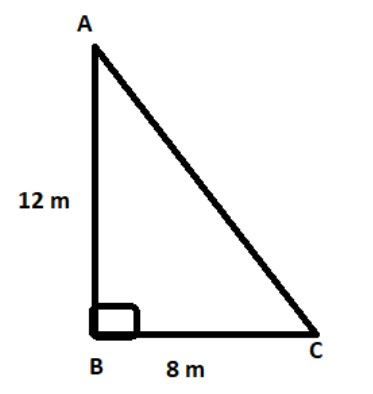
This is the right angled triangle. Let $\angle ACB = \theta$
We use the trigonometry ratio $\tan \theta$ as,
$\Rightarrow \tan \theta = \dfrac{{{\text{perpendicular}}}}{{base}}$
$\Rightarrow \tan \theta = \dfrac{{AB}}{{BC}}$
Substituting the values of length of AB and BC, we get
$\tan \theta = \dfrac{{12}}{8}$…. (1)
Now we will draw another $\vartriangle PQR$ for the tower. Tower casts a shadow of$40$m long on the ground which is at the same time of the first. Since both shades are happening at the same time of the day. So, angles $\angle ACB\;and\;\angle PRQ$ both will be the same as $\theta$ , as in the first triangle.

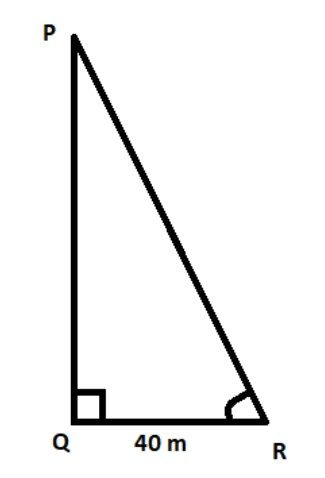
Now, assume the height of the tower is h.
So, in $\vartriangle PQR$, we use trigonometry ratio $\tan \theta$ , as $\angle PRQ = \theta$ ,
So,
$\Rightarrow \tan \theta = \dfrac{{{\text{perpendicular}}}}{{base}}$
$\Rightarrow \tan \theta = \dfrac{{PQ}}{{RQ}}$
Now put value of$\tan \theta$from equation (1) , and other terms , we get
$\dfrac{{12}}{8} = \dfrac{h}{{40}}$
Solving it, we get
$h = \dfrac{{12 \times 40}}{8} \\\ \Rightarrow h = 60 \\\$
$\therefore$ Height of the tower is 60 meters.

Note: For geometrical shapes, especially in triangles, trigonometry ratios are very much applicable, for making relationship among the sides and angles of the triangle. There are six such trigonometry ratios have been defined. These are $\sin \theta ,\;\cos \theta ,\;\tan \theta ,\;\sec \theta ,\;\cos ec\theta ,\;and\;\cot \theta .$.Students should remember the trigonometric ratios and formulas for solving these types of problems.