Question

A vertical rod of length $l$ is moved with constant velocity $v$ towards the east. The vertical component of the earth’s magnetic field is $B$ and angle of dip is $\theta$ . The induced emf in the rod is:
(A) $Blv\cot \theta$
(B) $Blv\sin \theta$
(C) $Blv\tan \theta$
(D) $Blv\cos \theta$

Answer 1

Hint In electromagnetic induction when a conductor is moving with a certain velocity in the presence of a magnetic field then the voltage will be generated across the conductor and this is called the induced emf. This takes place due to a variation in the flux which is linked with that conductor. This problem is related to the induced emf.

Formula used
$\Delta e = \left( {\overrightarrow v \times \overrightarrow B } \right).\overrightarrow l$

Complete step-by-step solution
We have a term, the motional emf which is induced through the motion of a body in a constant magnetic field. The emf produced in this case is motional emf and its formula usually is given by
$\Delta e = \left( {\overrightarrow v \times \overrightarrow B } \right).\overrightarrow l$
Here $e$ is the induced motional emf and it is to be noted that the magnetic field $B$ and velocity of the rod $v$ and the length of the rod $l$ should be mutually perpendicular to each other.

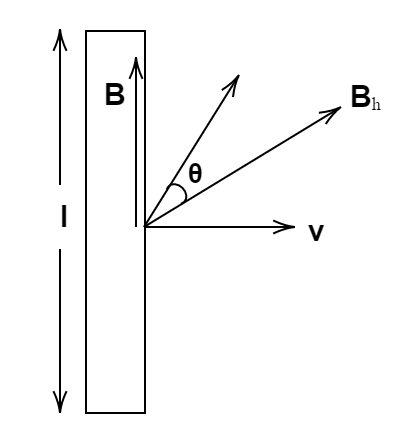
From the above figure, we can conclude that the magnetic force which is responsible for the induction of emf is the horizontal component of the magnetic field only, say ${B_H}$. Therefore,
$\Delta e = v{B_H}l\sin {90^ \circ } = v{B_H}l$ ............$\left( 1 \right)$
It is specified in the question that the horizontal component of the earth’s magnetic field is making an angle $\theta$.
Now, $\tan \theta = \dfrac{B}{{{B_H}}}$
Taking ${B_H}$ to the left-hand side we get,
${B_H} = \dfrac{B}{{\tan \theta }} = B\cot \theta$
Substitute the value of ${B_H}$ in equation $\left( 1 \right)$ , so the induced emf comes to be:
$\Delta e = v.{B_H}.l$
$\Rightarrow \Delta e = v.B\cot \theta .l$
On rearranging the terms we get,
$\Delta e = Blv\cot \theta$
As a result, the emf induced in the rod is $Blv\cot \theta$ .

Hence, the correct answer is option (A) $Blv\cot \theta$.

Note The angle made in the magnetic meridian between the sum of the magnetic field of the earth and the surface of the earth (horizontal component) is referred to as the dip angle. For field maps and geological fields, the dip angle plays a significant role. The dip assists in ensuring the steepest angle of descent relative to a horizontal plane for every tilted bed.