Question

A vertical rod of length $l$ is moved with a constant velocity $v$ towards east. The vertical component of Earth’s magnetic field is $B$ and angle f dip is $\theta$. The induced emf in the rod is:

Answer 1

Use the formula for the emf induced in a rod. This formula gives the relation between the emf induced in the rod, length of the rod, velocity of the rod and angle between the velocity of rod and magnetic field. Hence, calculate the emf induced in the rod due to the vertical component of the Earth’s magnetic field and horizontal component of the Earth’s magnetic field.

Formula used:
The induced emf $e$ in a rod is given by
$e = Blv\sin \theta$ …… (1)
Here, $v$ is the velocity of the rod, $B$ is the magnetic field, $l$ is length of the rod and $\theta$ is the angle between the velocity of the rod and the magnetic field.

Complete step by step answer:
We have given that a vertical rod of length $l$ is moved with a constant velocity $v$ towards east.We have also given that the vertical component of the Earth’s magnetic field is $B$ and the angle of dip is $\theta$. We have asked to calculate the induced emf in the rod.Let us first draw the diagram of the rod and components of the Earth’s magnetic field.

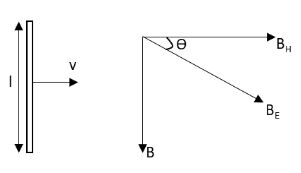
In the above figure, ${B_E}$ is the Earth’s magnetic field, ${B_H}$ is the horizontal component of the Earth’s magnetic field and $B$ is the vertical component of the Earth’s magnetic field. The angle of dip and the direction of velocity of the rod are also shown in the above figure.Let us now calculate the induced emf in the rod.

According to equation (1), the induced emf due to the vertical component of the Earth’s magnetic field is zero as the angle between the velocity of the rod and vertical component of the Earth’s magnetic field when the rod is moving towards the east is $0^\circ$.
From the above figure, we can write
$\tan \theta = \dfrac{B}{{{B_H}}}$
$\Rightarrow {B_H} = \dfrac{B}{{\tan \theta }}$
$\Rightarrow {B_H} = B\cot \theta$
Hence, we can say that the emf induced in the rod is only due to the horizontal component of the Earth’s magnetic field.

We can write the equation (1) as
$e = {B_H}lv\sin \theta$
The angle between the horizontal component of the Earth’s magnetic field and velocity of the rod is $90^\circ$.
Substitute $90^\circ$ for $\theta$ in the above equation.
$e = {B_H}lv\sin 90^\circ$
$\Rightarrow e = {B_H}lv\left( 1 \right)$
$\Rightarrow e = {B_H}lv$
Substitute $B\cot \theta$ for ${B_H}$ in the above equation.
$\Rightarrow e = \left( {B\cot \theta } \right)lv$
$\therefore e = Blv\cot \theta$

Hence, the induced emf in the rod is $Blv\cot \theta$.

Note: The students may get confused that initially the velocity of the rod is perpendicular to the vertical component of the Earth’s magnetic field then why the induced emf due to this component is zero. But the students should keep in mind that the angle between the velocity of the rod and vertical component of the Earth’s magnetic field is zero during the motion of the rod.