Question

A vertical post 15 ft high is broken at a certain height at its upper part, not completely separated, meets the ground at an angle of 30. Find the height at which the post is broken.
${\text{A}}{\text{. 10 ft}} \\\ {\text{B}}{\text{. 5 ft}} \\\ {\text{C}}{\text{. 15}}\sqrt {\text{3}} \left( {{\text{2 - }}\sqrt {\text{3}} } \right){\text{ ft}} \\\ {\text{D}}{\text{. 5}}\sqrt {\text{3}} {\text{ ft}} \\\$

Answer 1

“In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides”, this is the Pythagoras theorem. The sides of this triangle have been named as Perpendicular, Base and Hypotenuse. Here, the hypotenuse is the longest side, as it is opposite to the angle $90^\circ .$
Approaching by diagram use of Pythagoras theorem: ${H^2} = {B^2} + {P^2}$
Substituting$H = L$,$B = A$and $P = K$, we have:

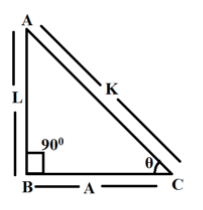
${L^2} + {A^2} = {K^2}$ and by trigonometric ratios:
$\sin \theta = \dfrac{L}{K}$; $\cos \theta = \dfrac{A}{K}$; $\tan \theta = \dfrac{L}{K}$

Complete step-by -step solution:
It is given that the height of vertical post $= 15ft$
After breaking meets the ground at an angle $= {30^0}$

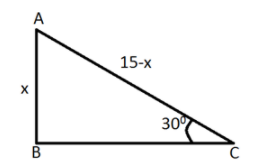
Let us assume the height at which the post is broken as $x$
Now height between the broken point and top of the post will be $15 - x$ (acts like the hypotenuse).
Now by diagram using Pythagoras theorem in triangle ABC as:

$$\Rightarrow \sin {30^0} = \dfrac{{AB}}{{AC}} \\\ \Rightarrow \dfrac{1}{2} = \dfrac{x}{{15 - x}} \\\ \Rightarrow 15 - x = 2x \\\ \Rightarrow 3x = 15 \\\ \Rightarrow x = 5{\text{ ft}} \\\$$

Hence, the height at which the post is broken is $x = 5ft$

Hence the correct answer is option (B).

Note: In this particular question students may get confused here with the hypotenuse of the triangle, which is the broken arm of the post and not the remaining part of the post.