Question
Question: A vertical pole of height 5.60 m casts a shadow of length 3.20 m on the horizontal earth surface. Un...
A vertical pole of height 5.60 m casts a shadow of length 3.20 m on the horizontal earth surface. Under the similar conditions and at the same time, find the length of the shadow cast by another vertical pole of height 10.5 m.
Solution
The vertical pole and the shadow cast by it on the horizontal ground form a right angle. We will examine the right angled triangle formed by the first pole and its shadow. Then we will use the given information about the similar conditions and the same time to construct a triangle which will have one side as the second pole. We will show that these two triangles are similar. Then by taking the ratio of the height and the shadow of the pole, we will calculate the length of the shadow cast by the second pole.
Complete step by step answer:
Let us draw a rough diagram of the two poles and their shadows.
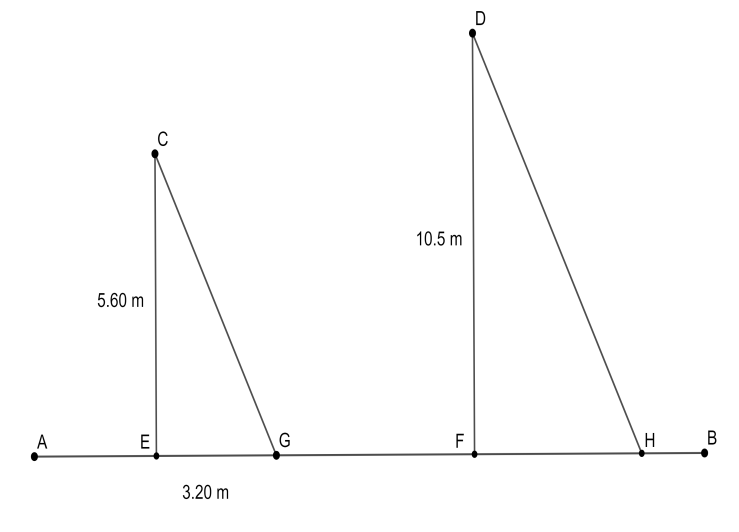
Segment CE is the pole that has height 5.60 m. It casts a shadow (segment EG) of length 3.20 m on the ground. Since the pole is vertically upright, we have ∠CEG=90∘. The angle formed by the ray of light (segment CG) with the pole CE is ∠GCE, at a certain time. Now, we will consider the second pole, that is segment DF, which has the height 10.5 m. The angle made by the pole DF on the ground is a right angle, since the pole is vertically upright.
The shadow cast by pole DF is shown as segment FH in the diagram. We have the information that the shadow FH has been cast by the pole DF under similar conditions and the same time as that of shadow EG which is cast by pole CE. This implies that segment CG and segment DH are parallel rays of light from a distant source at the same time. As we already know that the vertical poles are parallel to each other, we can conclude that ∠GCE=∠HDF.
Now, consider the ΔCEG and ΔDFH. We have ∠CEG=∠DFH=90∘ and from the above argument, ∠GCE=∠HDF. Therefore, the third angle of these two triangles would have to be equal, so that the sum of all angles of both the triangles will be 180∘. Therefore, by the AAA test, we conclude that ΔCEG∼ΔDFH.
Hence, we can now take the ratio of the heights of the poles and their shadows in the following manner,
EGCE=FHDF .
We know that CE=5.60, EG=3.20 and DF=10.5. Substituting these values in the above equation, we get
3.205.60=FH10.5
Rearranging and simplifying the above equation, we get the following,
FH=10.5×5.603.20=6.
Therefore, the length of the shadow cast by the pole of height 10.5 m is 6 m.
Note:
Drawing rough diagrams is very useful for such types of questions. The similarity of the triangles is the main part in this question. We should be familiar with the different tests involving sides and angles of triangles to prove the similarity of two triangles. It is beneficial to label the diagram so that there is no possibility of confusion while writing the ratios of similar sides.
