Question

A vertical pole has a red mark at some height. A stone is projected from a fixed point on the ground. When projected at an angle of $45^\circ$ it hits the pole orthogonally $1{\rm{ m}}$ above the mark. When projected with a different velocity at an angle of ${\tan ^{ - 1}}\left( {{3 {\left/{\vphantom {3 4}} \right.} 4}} \right)$, it hits the pole orthogonally $1.5{\rm{ m}}$ below the mark. Find the velocity and angle of projection so that it hits the mark orthogonally to the pole. $\left[ {g = 10{{\rm{m}} {\left/{\vphantom {{\rm{m}} {{\rm{se}}{{\rm{c}}^2}}}} \right.} {{\rm{se}}{{\rm{c}}^2}}}} \right]$

Answer 1

It is said that the stone hits the pole orthogonally, which means that stone is at the maximum point of the trajectory. We will be using the relationship of range and maximum height which gives the relation in the form of the angle of projection, velocity and acceleration due to gravity.

Complete step by step answer:
Let H be the height of the red mark on the pole from the ground.
Given:
The angle at which stone is thrown the first time is ${\theta _1} = 45^\circ$.
The angle at which stone is thrown the second time is ${\theta _2} = {\tan ^{ - 1}}\left( {\dfrac{3}{4}} \right) = 36.87^\circ$.

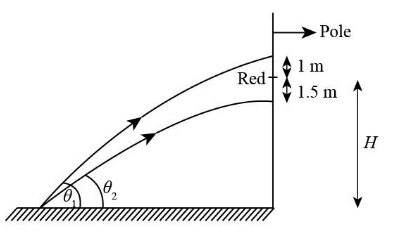
It is given that when a stone is projected at an angle of $45^\circ$ it hits the pole orthogonally $1{\rm{ m}}$ above the mark so we can say that the maximum height of the stone is $\left( {H + 1} \right)$ which is equal to:
$H + 1 = \dfrac{{u_1^2{{\sin }^2}{\theta _1}}}{{2g}}$……(1)
Here ${u_1}$ is the velocity of the stone when projected with angle ${\theta _1}$.
Substitute $45^\circ$ for ${\theta _1}$ in equation (1).

H + 1 = \dfrac{{u_1^2{{\sin }^2}\left( {45^\circ } \right)}}{{2g}}\\\ \Rightarrow H + 1 = \dfrac{{u_1^2}}{{4g}} $$……(2) The expression for range when stone is thrown at angle $${\theta _1}$$. $$R = \dfrac{{u_1^2\sin 2{\theta _1}}}{g}$$……(3) Substitute $$45^\circ $$ for $${\theta _1}$$ in equation (3).

R = \dfrac{{u_1^2\sin 2\left( {45^\circ } \right)}}{g}\\
\Rightarrow R = \dfrac{{u_1^2}}{g}

From equation (2) and equation (4), we can write: $$4\left( {H + 1} \right) = R$$……(5) When the stone is projected at an angle of $$36.87^\circ $$ it hits the pole orthogonally $$1.5{\rm{ m}}$$ below the mark so we can say that the maximum height of the stone is $$\left( {H - 1.5} \right)$$ which is equal to: $$H - 1.5 = \dfrac{{u_2^2{{\sin }^2}{\theta _2}}}{{2g}}$$……(6) Here $${u_2}$$ is the velocity of the stone when projected with angle $${\theta _2}$$. Substitute $$36.87^\circ $$ for $${\theta _2}$$ in equation (6).

H - 1.5 = \dfrac{{u_2^2{{\sin }^2}\left( {36.87^\circ } \right)}}{{2g}}\\
\Rightarrow H - 1.5 = 0.18\left( {\dfrac{{u_2^2}}{g}} \right)

The expression for range when the stone is thrown at an angle $${\theta _2}$$. $$R = \dfrac{{u_1^2\sin 2{\theta _2}}}{g}$$……(8) Substitute $$36.87^\circ $$ for $${\theta _2}$$ in equation (8).

R = \dfrac{{u_2^2\sin 2\left( {36.87^\circ } \right)}}{g}\\
\Rightarrow R = 0.96\left( {\dfrac{{u_2^2}}{g}} \right)

From equation (7) and equation (9), we can write: $$5.33\left( {H - 1.5} \right) = R$$……(10) Substitute $$4\left( {H + 1} \right)$$ for R from equation (5) in equation (10).

5.33\left( {H - 1.5} \right) = 4\left( {H + 1} \right)\\
\Rightarrow 5..33H - 4H = 4 + 7.995\\
\Rightarrow H = 9{\rm{ m}}

Substitute $$9{\rm{ m}}$$ for H in equation (5).

R = 4\left( {9 + 1} \right)\\
\Rightarrow R = 40{\rm{ m}}

Write the expression for maximum height when the stone is thrown at an angle $$\theta $$ so that it hits the red mark. $$H = \dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}}$$ Substitute $$9{\rm{ m}}$$ for R in the above equation.

9{\rm{ m}} = \dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}}\\
\Rightarrow 9{\rm{ m}} = \dfrac{{{u^2}\sin \theta \sin \theta }}{g}$……(11) Write the expression for range when the stone is thrown at an angle$\theta $so that it hits the red mark.$R = \dfrac{{{u^2}\sin 2\theta }}{g}$Substitute$40{\rm{ m}}$$ for R in the above expression.

40{\rm{ m}} = \dfrac{{{u^2}\sin 2\theta }}{g}\\\ \Rightarrow 20{\rm{ m}} = \dfrac{{{u^2}\sin \theta \cos \theta }}{g} $$……(12) From equation (11) and equation (12), we can write:

\tan \theta = \dfrac{{18}}{{20}}\\
\Rightarrow\theta = 41.98^\circ

Substitute $$41.98^\circ $$ for $$\theta $$ and $$10{{\rm{m}} {\left/ {\vphantom {{\rm{m}} {{\rm{se}}{{\rm{c}}^2}}}} \right. } {{\rm{se}}{{\rm{c}}^2}}}$$ for g in equation (12)

20{\rm{ m}} = \dfrac{{{u^2}\sin \left( {41.98^\circ } \right)\cos \left( {41.98^\circ } \right)}}{{10{{\rm{m}} {\left/
{\vphantom {{\rm{m}} {{\rm{se}}{{\rm{c}}^2}}}} \right.
} {{\rm{se}}{{\rm{c}}^2}}}}}\\
\Rightarrow {u^2} = 402.22{\rm{ }}{{{{\rm{m}}^2}} {\left/
{\vphantom {{{{\rm{m}}^2}} {{\rm{se}}{{\rm{c}}^2}}}} \right.
} {{\rm{se}}{{\rm{c}}^2}}}\\
\therefore u = 20.05{{{\rm{ m}}} {\left/
{\vphantom {{{\rm{ m}}} {{\rm{sec}}}}} \right.
} {{\rm{sec}}}}

**Therefore, we can say that $$41.98^\circ $$ is the angle of projection and $$20.05{{{\rm{ m}}} {\left/{\vphantom {{{\rm{ m}}} {{\rm{sec}}}}} \right.} {{\rm{sec}}}}$$ velocity required by the stone to hit the red mark.** **Note:** Understand the given statement carefully and draw a diagram for it so that there will be no confusion regarding various mark points. Also, it would be an advantage if we remember various relations of projectile motion, especially range and maximum height.