Question
Question: A vertical lamp post of height 9 meters stands at the corner of a rectangular field. The angle of ev...
A vertical lamp post of height 9 meters stands at the corner of a rectangular field. The angle of evolution of its top from the farthest corner is 30∘, which from another corner it is 45∘, the area of the field is
A.92meter2\B.813meter2C.812meter2\D.93meter2
Solution
Hint: First of all, we will draw the diagram and then, by using the trigonometric ratios, we will find the side of a rectangle, we will be using the tangent ratio which is the ratio of perpendicular to base. Value of tanθat standard angles such as tan30∘=31andtan45∘=1 must be known and used in the solution and we will use the formula of area of rectangle, which is equal to the product of length and breadth of a rectangle.
Complete step-by-step answer:
We have been given that, a lamp post of height 9 meters stands at the corner of a rectangular field. Also, the angle of elevation of its top from farthest corner is 30∘ while from another corner is 45∘
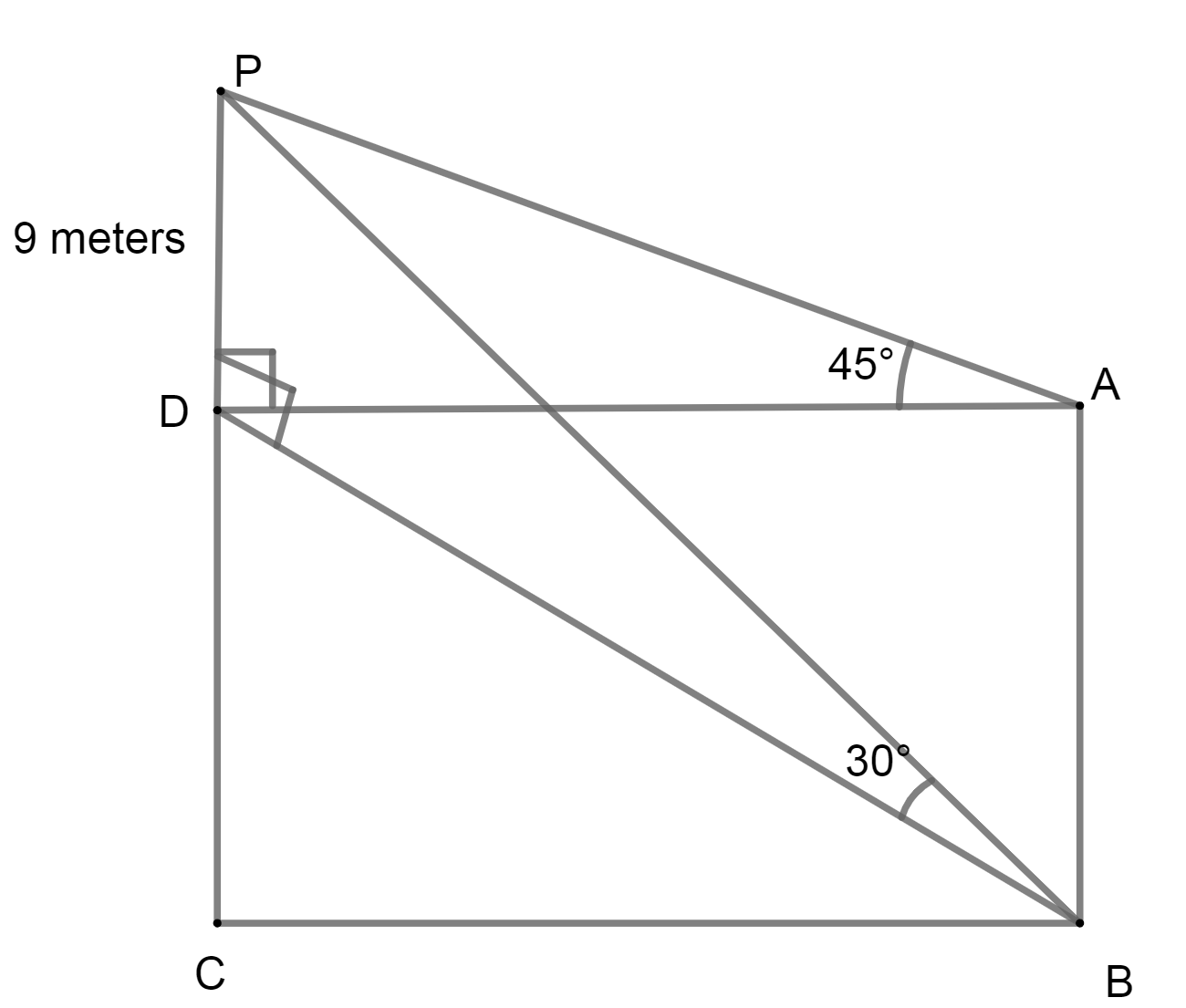
We have PD= 9 meters
Now, in ΔAOP,
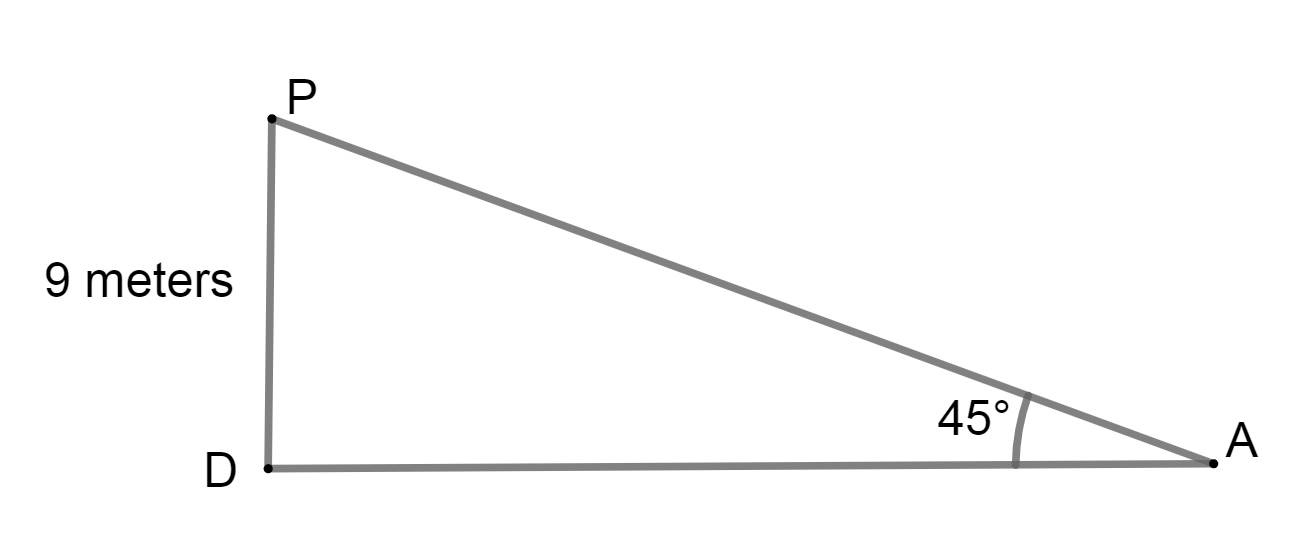
tanA=ADPD ⇒tan45∘=AD9
We know that, tan45∘=1
⇒1=AD9 ⇒AD=9meter
Again, inΔPDB,
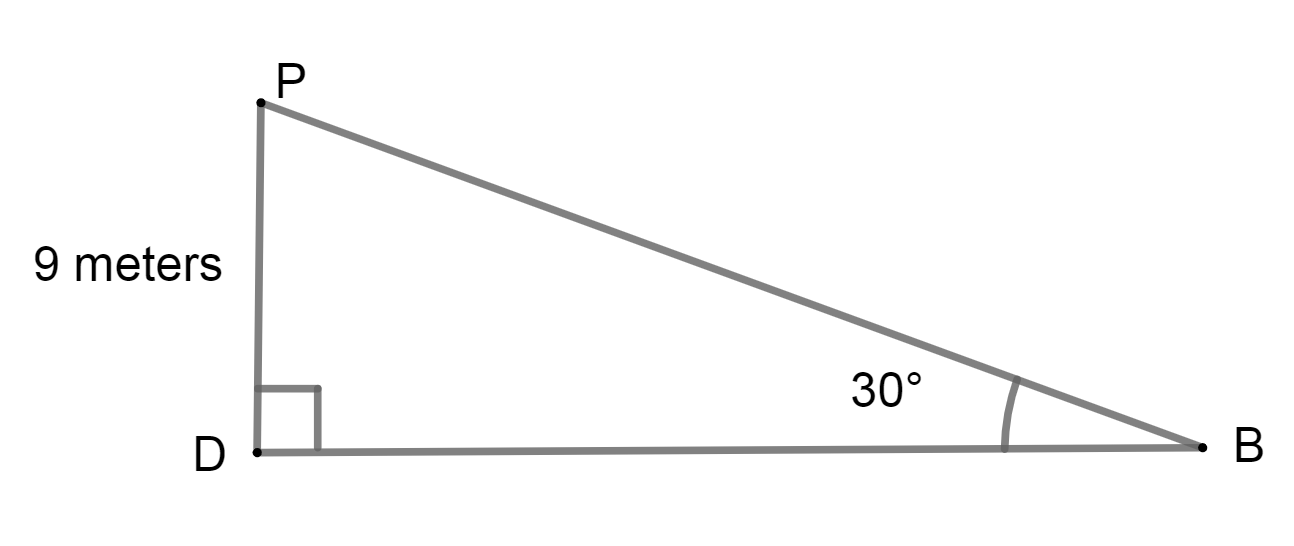
tanB=BDPD ⇒tan30∘=BD9
We know that, tan30∘=31
⇒31=BD9 ⇒BD=93meter
Now, 2n right angled triangle i.e. ΔDAB by using Pythagoras theorem, we get
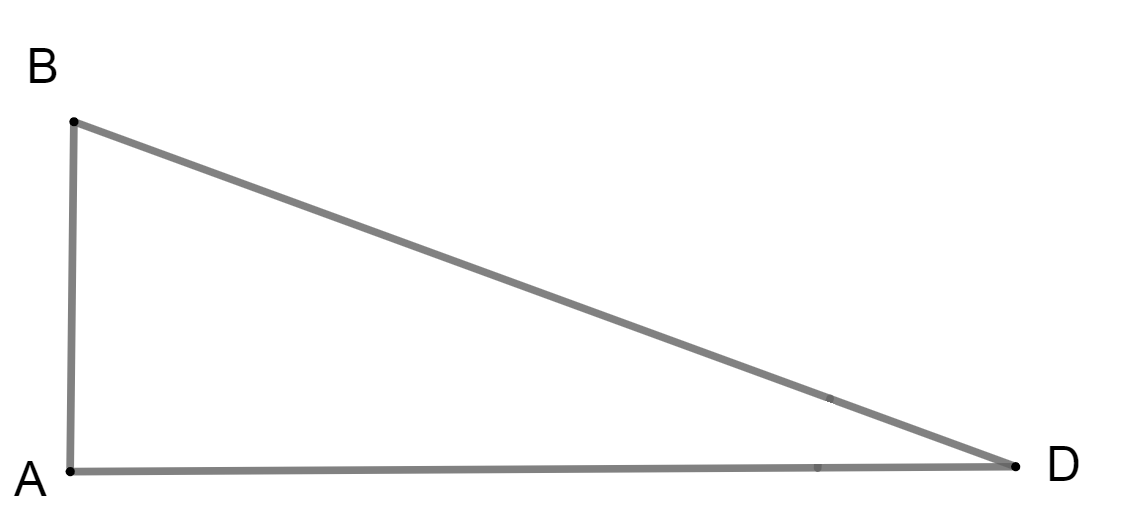
AB2+AD2=BD2\AB2+92=(93)2\AB2+81=243\AB2=243−81\AB2=162\AB=162\AB=92meter
We know that, area of a rectangle is equal to the product of its length and breadth.
We have length = AD = 9 meter and
Breadth = AB = 92meter
So,
Area=AD×AB ⇒9×92m2 ⇒812m2
Therefore, the correct option is C.
Note: It is very important to draw the diagram in height and distance problem as it becomes easy to visualize the things, which helps us to proceed further in the question. In this question, we might take tan30∘ as 3 and get different answers. We have to find the sides of the rectangle, so we can use any technique to obtain the length. We must try to figure out how to proceed and then start calculating, this saves time and efforts too.
