Question

A vertical lamp post, 6 m high, stands at a distance of 2m from a wall, 4m high. A 1.5m tall man starts to walk away from the wall on the other side of the wall, in line with the lamp-post. The maximum distance to which the man can walk remaining in the shadow is
a.$\dfrac{5}{2}m$
b.$\dfrac{3}{2}m$
c.4m
d.None of these

Answer 1

Hint: First of all, draw the appropriate figure with the help of data provided in the question. PQ as the height of the vertical lamp, AB as the height of the wall, and CD as the height of the man. Now, join the points P, Q, and R. We have $\Delta ABR\simeq \Delta CDR$ and $\Delta PQR\simeq \Delta ABR$ . Using this, we can write $\dfrac{BR}{DR}=\dfrac{AB}{CD}=\dfrac{4}{1.5}=\dfrac{8}{3}$ and $\dfrac{PQ}{AB}=\dfrac{QR}{BR}$ . Now, solve these two equations and get the values of length BR and DR. The maximum distance to which the man can walk remaining in the shadow is BR-DR. Solve it further.

Complete step-by-step answer:

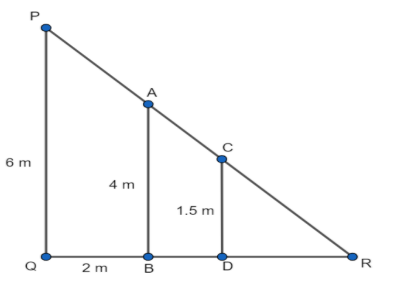
According to the figure we have, PQ as the height of the vertical lamp, AB as the height of the wall, and CD as the height of the man.
The distance between the wall and vertical lamp = QB = 2 m.
The height of the vertical lamp = PQ = 6 m.
The height of the wall = AB = 4 m.
The height of the man = CD = 1.5 m.
In the $\Delta ABR$ and $\Delta CDR$ , we have
$\angle ABR=\angle CDR={{90}^{0}}$
$\angle ARB=\angle CRD$ (angles common in both triangles)
If any two triangles have two equal angles then the third angle of both triangles is also equal.
So, $\angle BAR=\angle DCR$ .
So, $\Delta ABR\simeq \Delta CDR$ .
We have, $\Delta ABR\simeq \Delta CDR$ ,
$\dfrac{BR}{DR}=\dfrac{AB}{CD}=\dfrac{4}{1.5}=\dfrac{8}{3}$ …………………..(1)
In the $\Delta ABR$ and $\Delta PQR$ , we have
$\angle ABR=\angle PQR={{90}^{0}}$
$\angle ARB=\angle PRQ$ (angles common in both triangles)
If any two triangles have two equal angles then the third angle of both triangles is also equal.
So, $\angle BAR=\angle QPR$ .
So, $\Delta PQR\simeq \Delta ABR$
We have, $\Delta PQR\simeq \Delta ABR$ ,

& \dfrac{PQ}{AB}=\dfrac{QR}{BR} \\\ & \Rightarrow \dfrac{6}{4}=\dfrac{BQ+BR}{BR} \\\ & \Rightarrow \dfrac{3}{2}=\dfrac{2+BR}{BR} \\\ & \Rightarrow 3BR=4+2BR \\\ \end{aligned}$$ $$\Rightarrow BR=4$$ …………………..(2) From equation (1) and equation (2), we get $$\begin{aligned} & \dfrac{4}{DR}=\dfrac{8}{3} \\\ & \Rightarrow \dfrac{3}{2}=DR \\\ \end{aligned}$$ From the figure, we can see that BD = BR – DR = $$4-\dfrac{3}{2}=\dfrac{5}{2}$$ . So, the maximum distance to which the man can walk remaining in the shadow is $$\dfrac{5}{2}$$ . Hence, the correct option is A. Note: In this question, one can think that the man walks between the wall and the vertical lamp post which is wrong. As in the question, it is given that the man walks away from the wall to the other side of the wall, so we can’t think that the man walks between the wall and the vertical lamp.