Question

A vertical cylinder is divided into two parts by a frictionless piston in the ratio 5:4. The piston is free to slide along the length of the vessel and the length of the vessel is $90{\text{cm}}$. Each of the two parts of the vessel contains $0 \cdot 1{\text{mol}}$ of an ideal gas and the temperature of the gas is $300{\text{K}}$. Find the mass of the piston.
A) $14{\text{kg}}$
B) $12 \cdot 7{\text{kg}}$
C) $16{\text{kg}}$
D) $15{\text{kg}}$

Answer 1

The gas in the lower part of the cylinder will exert a force on the piston in the upward direction while the gas in the upper part of the cylinder exerts a force on the piston in the downward direction. Also, the weight of the piston will be directed downwards. However, at equilibrium, the net force acting on the piston will be zero.

Formulas used:
The force acting on a container filled with gas is given by, $F = PA$ where $P$ is the pressure exerted by the gas and $A$ is the area of the container.
The ideal gas equation is given by, $PV = nRT$ where $P$ is the pressure, $V$ is the volume, $n$ is the number of moles present in the sample of gas, $R$ is the gas constant and $T$ is the temperature of the gas.
The volume of a container is given by, $V = Al$ where $A$ is the area of the container and $l$ is its length.

Complete step by step answer:

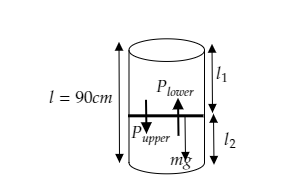
In the above figure, we see that the piston divides the length of the cylinder into a ratio of 5 : 4.
The total length of the vessel is given to be $l = 90{\text{cm}}$ .
Now, ${l_1}$ and ${l_2}$ are the lengths of the upper part and lower part respectively.
The number of moles present in each part is given to be $n = 0 \cdot 1{\text{mol}}$ .
The temperature of the gas in each part is given to be $T = 300{\text{K}}$ .
In the figure, ${P_{lower}}$ is the pressure exerted by the gas in the lower part and ${P_{upper}}$ is the pressure exerted by the gas in the upper part.
The weight of the piston will be $W = mg$.

It is given that $\dfrac{{{l_1}}}{{{l_2}}} = \dfrac{5}{4} \Rightarrow {l_1} = \dfrac{{5{l_2}}}{4}$ .
Also, we have ${l_1} + {l_2} = l = 90{\text{cm}}$
Then substituting for ${l_1} = \dfrac{{5{l_2}}}{4}$ in the above relation we get, $\dfrac{{5{l_2}}}{4} + {l_2} = 90{\text{cm}}$
$\Rightarrow \dfrac{{9{l_2}}}{4} = 90$ or ${l_2} = \dfrac{{4 \times 90}}{9} = 40{\text{cm}}$
Then ${l_1} = \dfrac{{5 \times 40}}{4} = 50{\text{cm}}$ .
Thus the lengths of the upper part and lower part are respectively, ${l_1} = 50{\text{cm}}$ and ${l_2} = 40{\text{cm}}$ .

The ideal gas equation is given by, $PV = nRT$ where $P$ is the pressure, $V$ is the volume, $n$ is the number of moles present in the sample of gas, $R$ is the gas constant and $T$ is the temperature of the gas.
Then from the ideal gas equation, the pressure in the lower part can be expressed as ${P_{lower}} = \dfrac{{nRT}}{{{V_2}}} = \dfrac{{nRT}}{{{A_2}{l_2}}}$ ------- (1)
Similarly, the pressure in the upper part can be expressed as ${P_{upper}} = \dfrac{{nRT}}{{{V_1}}} = \dfrac{{nRT}}{{{A_1}{l_1}}}$ ------- (2)

The net force acting on the piston at equilibrium can be expressed as ${F_1} + W = {F_2}$ ------ (3)
where ${F_1}$ is the force on the piston due to the upper part, ${F_2}$ is the force on the piston due to the lower part and $W$ is the weight of the piston.
Then substituting for ${F_1} = {P_{upper}}{A_1}$ , ${F_2} = {P_{lower}}{A_2}$ and $W = mg$ in equation (3) we get, ${P_{upper}}{A_1} + mg = {P_{lower}}{A_2}$ --------- (4)
Now substituting equations (1) and (2) in (4) we get, $\dfrac{{nRT{A_2}}}{{{A_2}{l_2}}} + mg = \dfrac{{nRT{A_1}}}{{{A_1}{l_1}}}$
$\Rightarrow m = \dfrac{{nRT}}{g}\left( {\dfrac{1}{{{l_1}}} - \dfrac{1}{{{l_2}}}} \right)$ ------------- (5)
Substituting for $n = 0 \cdot 1{\text{mol}}$ , $T = 300{\text{K}}$ , ${l_1} = 50{\text{cm}}$ , ${l_2} = 40{\text{cm}}$ , $g = 9 \cdot 8{\text{m}}{{\text{s}}^{ - 2}}$ and $R = 8 \cdot 31{\text{J}}{{\text{K}}^{ - 1}}{\text{mo}}{{\text{l}}^{ - 1}}$ in equation (5) we get, $m = \dfrac{{0 \cdot 1 \times 8 \cdot 31 \times 300}}{{9 \cdot 8}}\left( {\dfrac{1}{{0 \cdot 5}} - \dfrac{1}{{0 \cdot 4}}} \right) = 12 \cdot 7{\text{kg}}$

Therefore, the mass of the piston is $m = 12 \cdot 7{\text{kg}}$. So the correct option is B.

Note:
At equilibrium, as the net force acting on the piston is zero, the piston will not move. While substituting values in any equation make sure that the physical quantities are expressed in their respective S.I. units. If not, then the necessary conversion of units must be done. Here the lengths of the two parts are converted to meters during their substitution in equation (5).