Question

A vertex of a square is at the origin and its one side lies along the line $3x-4y-10=0$ . Find the area of the square.

Answer 1

Start by drawing the representative diagram of the situation given in the figure. As one of the sides of the square is $3x-4y-10=0$ and origin is not lying on this line but origin is one of the vertices. So, the origin must lie on the opposite side and the distance of the origin from the given line is equal to the side length of the square, and can be found using the formula $\left| \dfrac{a{{x}_{1}}+b{{y}_{1}}+c}{\sqrt{{{a}^{2}}+{{b}^{2}}}} \right|$ . Once you know the side length, square it to get the area of the square, as the area of the square is square of its side length.

Complete step-by-step answer :
Let us start the solution to the above question by drawing a representative diagram of the situation given in the question.

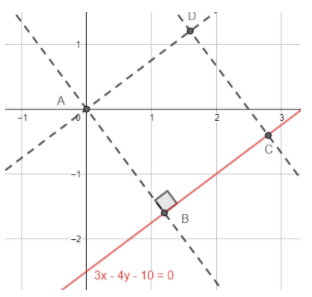
As one of the sides of the square is $3x-4y-10=0$ and origin is not lying on this line but origin is one of the vertices. So, the origin must lie on the opposite side and the distance of the origin from the given line is equal to the side length of the square. The same can be seen from the diagram also, that AB is the one of the sides of the square and is the distance between the origin and the line BC whose equation is $3x-4y-10=0$ .
Now to find the length of the side AB, we will use the formula of perpendicular distance of a point from a line. We know that the distance of the point $({{x}_{1}},{{y}_{1}})$ from the line ax+by+c=0 is $\left| \dfrac{a{{x}_{1}}+b{{y}_{1}}+c}{\sqrt{{{a}^{2}}+{{b}^{2}}}} \right|$ . Therefore, the perpendicular distance of (0,0) from $3x-4y-10=0$ is:
$\left| \dfrac{a{{x}_{1}}+b{{y}_{1}}+c}{\sqrt{{{a}^{2}}+{{b}^{2}}}} \right|=\left| \dfrac{-10}{\sqrt{{{3}^{2}}+{{4}^{2}}}} \right|=\dfrac{10}{\sqrt{25}}=\dfrac{10}{5}=2$
So, the side length of the square is 2 units. We know that the area of the square is equal to the square of its side.
$\text{Area of the square}={{a}^{2}}={{2}^{2}}=4\text{ uni}{{\text{t}}^{2}}$
Therefore, the area of the square is 4 sq units.

Note : If you want you can use the equation of the line to get the equation of the perpendicular line using the point that the product of the slopes of perpendicular line is -1, followed by using the point that the line will pass through the origin. The line opposite to the given line will be parallel to it, i.e. the slope will remain the same which means that only the constant part will change which can be found by putting the origin in the equation. This way you can draw all the results, but here you were asked only about the area so we didn’t use all these results.